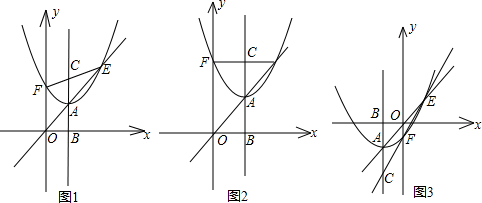
解:(1)∵拋物線頂點(h,m)在直線y=kx上,
∴m=kh;
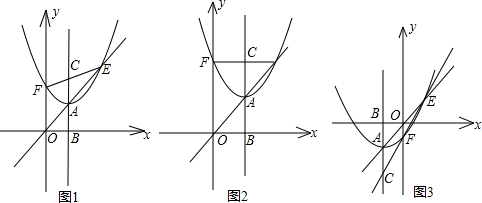
(2)方法一:解方程組
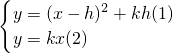
,
將(2)代入(1)得到:(x-h)
2+kh=kx,
整理得:(x-h)[(x-h)-k]=0,
解得:x
1=h,x
2=k+h,
代入到方程(2)y
1=hy
2=k
2+hk,
所以點E坐標是(k+h,k
2+hk),
當x=0時,y=(x-h)
2+m=h
2+kh,
∴點F坐標是(0,h
2+kh),
當EF和x軸平行時,點E,F的縱坐標相等,
即k
2+kh=h
2+kh,
解得:h=k(h=-k舍去,否則E,F,O重合),
此時點E(2k,2k
2),F(0,2k
2),C(k,2k
2),A(k,k
2),
∴AC:OF=k
2:2k
2=1:2.
方法二:當x=0時,y=(x-h)
2+m=h
2+kh,即F(0,h
2+kh),
當EF和x軸平行時,點E,F的縱坐標相等,
即點E的縱坐標為h
2+kh,
當y=h
2+kh時,代入y=(x-h)
2+kh,
解得x=2h(0舍去,否則E,F,O重合),
即點E坐標為(2h,h
2+kh),
將此點橫縱坐標代入y=kx得到h=k(h=0舍去,否則點E,F,O重合),
此時點E(2k,2k
2),F(0,2k
2),C(k,2k
2),A(k,k
2),
∴AC:OF=k
2:2k
2=1:2.
方法三:∵EF與x軸平行,
根據拋物線對稱性得到FC=EC,
∵AC∥FO,
∴∠ECA=∠EFO,∠FOE=∠CAE,
∴△OFE∽△ACE,
∴AC:OF=EC:EF=1:2.
(3)當點F的位置處于最低時,其縱坐標h
2+kh最小,
∵h
2+kh=[h
2+kh+(

)
2]-
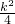
,
當h=
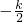
,點F的位置最低,此時F(0,-
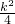
),
解方程組
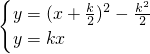
得E(

,
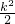
),A(-

,-
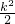
).
方法一:設直線EF的解析式為y=px+q,
將點E(

,
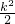
),F(0,-
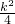
)的橫縱坐標分別代入得
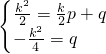
,
解得:p=
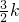
,q=-
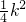
,
∴直線EF的解析式為y=
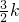
x-
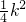
,
當x=-

時,y=-k
2,即點C的坐標為(-

,-k
2),
∵點A(-
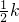
,-
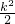
),
∴AC=
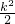
,而OF=
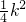
,
∴AC=2OF,即AC:OF=2.
方法二:∵E(

,
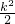
),A(-

,-
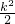
),
∴點A,E關于點O對稱,
∴AO=OE,
∵AC∥FO,
∴∠ECA=∠EFO,∠FOE=∠CAE,
∴△OFE∽△ACE,
∴AC:OF=AE:OE=2:1.
分析:(1)根據點A在直線y=kx上,即可得出h,m的關系式.
(2)當EF∥x軸時,根據拋物線的對稱性可知:FC=CE即C是EF的中點,那么AC就是三角形OEF的中位線,因此AC=

OF.
(也可通過聯立直線OA的解析式和拋物線的解析式得出E點的坐標,當EF∥x軸時,E、F縱坐標相同,以此來求出h,k的關系,進而表示出A、C、E、F四點坐標以此來求出AC與OF的比例關系).
(3)先求出F到最低位置時,函數的解析式(F位置最低時,縱坐標值最小).聯立兩函數的解析式求出A、E的坐標,然后根據相似三角形OEF和AEC求出OF,AC的比例關系.
點評:本題主要考查了函數圖象交點、相似三角形的性質等知識點.

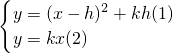 ,
, )2]-
)2]- ,
, ,點F的位置最低,此時F(0,-
,點F的位置最低,此時F(0,-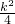 ),
),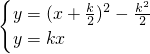
 ,
,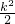 ),A(-
),A(- ,-
,-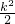 ).
). ,
,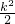 ),F(0,-
),F(0,-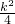 )的橫縱坐標分別代入得
)的橫縱坐標分別代入得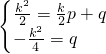 ,
,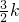 ,q=-
,q=-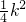 ,
,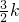 x-
x-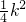 ,
, 時,y=-k2,即點C的坐標為(-
時,y=-k2,即點C的坐標為(- ,-k2),
,-k2),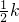 ,-
,-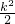 ),
),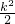 ,而OF=
,而OF=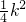 ,
, ,
,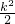 ),A(-
),A(- ,-
,- ),
), OF.
OF.

 在△ABC中,∠ACB=90°,AB=5,tanA=
在△ABC中,∠ACB=90°,AB=5,tanA= (2008•寶山區二模)已知∠AOB=45°,P是邊OA上一點,OP=4
(2008•寶山區二模)已知∠AOB=45°,P是邊OA上一點,OP=4