
【題目】如圖,二次函數![]() 的圖象過原點,與x軸的另一個交點為
的圖象過原點,與x軸的另一個交點為![]()
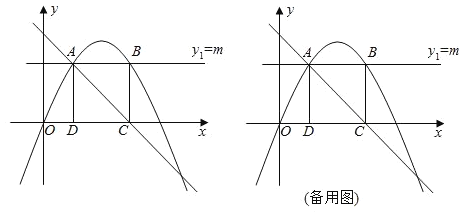
(1)求該二次函數的解析式;
(2)在x軸上方作x軸的平行線![]() ,交二次函數圖象于A、B兩點,過A、B兩點分別作x軸的垂線,垂足分別為點D、點C.當矩形ABCD為正方形時,求m的值;
,交二次函數圖象于A、B兩點,過A、B兩點分別作x軸的垂線,垂足分別為點D、點C.當矩形ABCD為正方形時,求m的值;
(3)在(2)的條件下,動點P從點A出發沿射線AB以每秒1個單位長度勻速運動,同時動點Q以相同的速度從點A出發沿線段AD勻速運動,到達點D時立即原速返回,當動點Q返回到點A時,P、Q兩點同時停止運動,設運動時間為t秒(![]() ).過點P向x軸作垂線,交拋物線于點E,交直線AC于點F,問:以A、E、F、Q四點為頂點構成的四邊形能否是平行四邊形.若能,請求出t的值;若不能,請說明理由.
).過點P向x軸作垂線,交拋物線于點E,交直線AC于點F,問:以A、E、F、Q四點為頂點構成的四邊形能否是平行四邊形.若能,請求出t的值;若不能,請說明理由.
【答案】(1)![]() ;(2)當矩形ABCD為正方形時,m的值為4;(3)以A、E、F、Q四點為頂點構成的四邊形能為平行四邊形,t的值為4或6.
;(2)當矩形ABCD為正方形時,m的值為4;(3)以A、E、F、Q四點為頂點構成的四邊形能為平行四邊形,t的值為4或6.
【解析】
(1)根據點的坐標,利用待定系數法即可求出二次函數的解析式;
(2)利用二次函數圖象上點的坐標特征求出點A,B的坐標,進而可得出點C,D的坐標,再利用正方形的性質可得出關于m的方程,解之即可得出結論;
(3)由(2)可得出點A,B,C,D的坐標,根據點A,C的坐標,利用待定系數法可求出直線AC的解析式,利用二次函數圖象上點的坐標特征及一次函數圖象上點的坐標特征可求出點E,F的坐標,由![]() 且以A、E、F、Q四點為頂點的四邊形為平行四邊形可得出
且以A、E、F、Q四點為頂點的四邊形為平行四邊形可得出![]() ,分
,分![]() ,
,![]() ,
,![]() 三種情況找出AQ,EF的長,由
三種情況找出AQ,EF的長,由![]() 可得出關于t的一元二次方程,解之取其合適的值即可得出結論.
可得出關于t的一元二次方程,解之取其合適的值即可得出結論.
(1)將![]() ,
,![]() 代入
代入![]() ,得:
,得: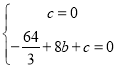 ,
,
解得![]() ,
,
∴該二次函數的解析式為![]() .
.
(2)當![]() 時,
時,![]() ,
,
解得:![]() ,
,![]() ,
,
∴點a的坐標為(![]() ,m),點b的坐標為(
,m),點b的坐標為(![]() ,m),
,m),
∴點d的坐標為(![]() ,0),點c的坐標為(
,0),點c的坐標為(![]() ,0).
,0).
∵矩形abcd為正方形,
∴![]() ,
,
解得:![]() ,(舍去),
,(舍去),![]() .
.
∴當矩形ABCD為正方形時,m的值為4.
(3)以A、E、F、Q四點為頂點構成的四邊形能為平行四邊形.
由(2)可知:點A的坐標為![]() ,點B的坐標為
,點B的坐標為![]() ,點C的坐標為
,點C的坐標為![]() ,點D的坐標為
,點D的坐標為![]() .
.
設直線AC的解析式為![]() ,
,
將![]() ,
,![]() 代入
代入![]() ,
,
得![]() ,
,
解得![]() ,
,
∴直線ac的解析式為![]() .
.
當![]() 時,
時,![]() ,
,![]()
∴點E的坐標為(![]() ,
,![]() ),點F的坐標為(
),點F的坐標為(![]() ,
,![]() -t+4).
-t+4).
∵以A、E、F、Q四點為頂點構成的四邊形為平行四邊形,且![]() ,
,
∴![]() ,分三種情況考慮:
,分三種情況考慮:
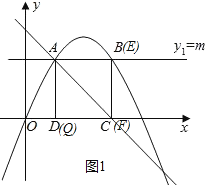
①當![]() 時,如圖1所示,
時,如圖1所示,![]() ,EF=
,EF=![]() ,
,
∴![]() ,解得:
,解得:![]() (舍去),
(舍去),![]() ;
;
②當![]() 時,如圖2所示,
時,如圖2所示,![]() ,EF=
,EF=![]() ,
,
∴![]() ,
,
解得:![]() (舍去),
(舍去),![]() ;
;
![]() ,
,![]() , EF=
, EF=![]() ,
,
![]() ,
,
解得![]() (舍去),
(舍去),![]() (舍去)
(舍去)
綜上所述,當以A、E、F、Q四點為頂點構成的四邊形為平行四邊形時,t的值為4或6


科目:初中數學 來源: 題型:
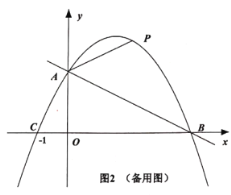
【題目】如圖,一次函數![]() 的圖像與坐標軸交于A、B兩點,點C的坐標為
的圖像與坐標軸交于A、B兩點,點C的坐標為![]() ,二次函數
,二次函數![]() 的圖像經過A、B、C三點.
的圖像經過A、B、C三點.
(1)求二次函數的解析式
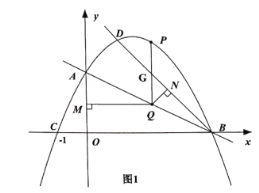
(2)如圖1,已知點![]() 在拋物線上,作射線BD,點Q為線段AB上一點,過點Q作
在拋物線上,作射線BD,點Q為線段AB上一點,過點Q作![]() 軸于點M,作
軸于點M,作![]() 于點N,過Q作
于點N,過Q作![]() 軸交拋物線于點P,當QM與QN的積最大時,求點P的坐標;
軸交拋物線于點P,當QM與QN的積最大時,求點P的坐標;
(3)在(2)的條件下,連接AP,若點E為拋物線上一點,且滿足![]() ,求點E的坐標.
,求點E的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
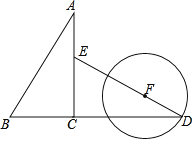
【題目】如圖,Rt△ABC中,∠ACB=90°,BC=3,tanA=![]() ,將Rt△ABC繞點C順時針旋轉90°得到△DEC,點F是DE上一動點,以點F為圓心,FD為半徑作⊙F,當FD=_____時,⊙F與Rt△ABC的邊相切.
,將Rt△ABC繞點C順時針旋轉90°得到△DEC,點F是DE上一動點,以點F為圓心,FD為半徑作⊙F,當FD=_____時,⊙F與Rt△ABC的邊相切.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,若二次函數y=ax2+bx+c(a≠0)圖象的對稱軸為x=1,與y軸交于點C,與x軸交于點A、點B(﹣1,0),則
①二次函數的最大值為a+b+c;
②a﹣b+c<0;
③b2﹣4ac<0;
④當y>0時,﹣1<x<3,其中正確的個數是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司2017年初剛成立時投資1000萬元購買新生產線生產新產品,此外,生產每件該產品還需要成本40元.按規定,該產品售價不得低于60元/件且不超過160元/件,且每年售價確定以后不再變化,該產品的年銷售量![]() (萬件)與產品售價
(萬件)與產品售價![]() (元)之間的函數關系如圖所示.
(元)之間的函數關系如圖所示.
(1)求![]() 與
與![]() 之間的函數關系式,并寫出
之間的函數關系式,并寫出![]() 的取值范圍;
的取值范圍;
(2)求2017年該公司的最大利潤?
(3)在2017年取得最大利潤的前提下,2018年公司將重新確定產品售價,能否使兩年共盈利達980萬元.若能,求出2018年產品的售價;若不能,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知BC⊥AC,圓心O在AC上,點M與點C分別是AC與⊙O的交點,點D是MB與⊙O的交點,點P是AD延長線與BC的交點,且ADAO=AMAP.
(1)連接OP,證明:△ADM∽△APO;
(2)證明:PD是ΘO的切線;
(3)若AD=24,AM=MC,求![]() 的值.
的值.
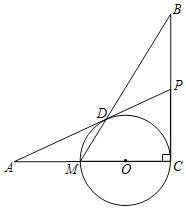
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,拋物線
,拋物線![]() 經過點
經過點![]() ,
,![]() .
.

(1)求點B的坐標和拋物線的解析式;
(2)M(m,0)為x軸上一個動點,過點M垂直于x軸的直線與直線AB和拋物線分別交于點P、N,
①點![]() 在線段
在線段![]() 上運動,若以
上運動,若以![]() ,
,![]() ,
,![]() 為頂點的三角形與
為頂點的三角形與![]() 相似,求點
相似,求點![]() 的坐標;
的坐標;
②點![]() 在
在![]() 軸上自由運動,若三個點
軸上自由運動,若三個點![]() ,
,![]() ,
,![]() 中恰有一點是其它兩點所連線段的中點(三點重合除外),則稱
中恰有一點是其它兩點所連線段的中點(三點重合除外),則稱![]() ,
,![]() ,
,![]() 三點為“共諧點”.請直接寫出使得
三點為“共諧點”.請直接寫出使得![]() ,
,![]() ,
,![]() 三點成為“共諧點”的
三點成為“共諧點”的![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某店在開學初用880元購進若干個學生專用科學計算器,按每個50元出售,很快就銷售一空,據了解學生還急需3倍這種計算器,于是又用2580元購進所需計算器,由于量大每個進價比上次優惠1元,該店仍按每個50元銷售,最后剩下4個按九折賣出.這筆生意該店共盈利( )元.
A.508 B.520 C.528 D.560
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com