
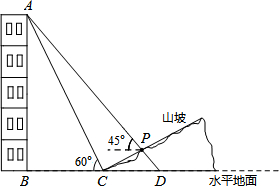
如圖,某人在山坡坡腳C處測得一座建筑物頂點A的仰角為60°,沿山坡向上走到P處再測得該建筑物頂點A的仰角為45°.已知BC=90米,且B、C、D在同一條直線上,山坡坡度為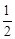 (即tan∠PCD=
(即tan∠PCD=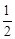 ).
).
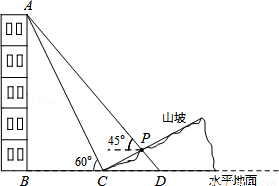
(1)求該建筑物的高度(即AB的長).
(2)求此人所在位置點P的鉛直高度.(測傾器的高度忽略不計,結果保留根號形式)
解:(1)過點P作PE⊥BD于E,PF⊥AB于F,
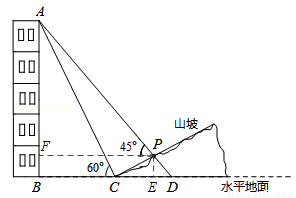
又∵AB⊥BC于B,∴四邊形BEPF是矩形。
∴PE=BF,PF=BE。
∵在Rt△ABC中,BC=90米,∠ACB=60°,
∴AB=BC•tan60°=90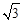 (米)。
(米)。
∴建筑物的高度為90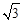 米。
米。
(2)設PE=x米,則BF=PE=x米,
∵在Rt△PCE中,tan∠PCD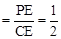 ,
,
∴CE=2x。
∵在Rt△PAF中,∠APF=45°,∴AF=AB﹣BF=90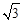 ﹣x,PF=BE=BC+CE=90+2x。
﹣x,PF=BE=BC+CE=90+2x。
又∵AF=PF,∴90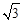 ﹣x=90+2x,解得:x=30
﹣x=90+2x,解得:x=30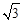 ﹣30,
﹣30,
答:人所在的位置點P的鉛直高度為(30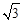 ﹣30)米。
﹣30)米。
【解析】
試題分析:(1)過點P作PE⊥BD于E,PF⊥AB于F,在Rt△ABC中,求出AB的長度即可。
(2)設PE=x米,則BF=PE=x米,根據山坡坡度為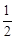 ,用x表示CE的長度,然后根據AF=PF列出等量關系式,求出x的值即可。
,用x表示CE的長度,然后根據AF=PF列出等量關系式,求出x的值即可。


科目:初中數學 來源: 題型:
| 1 |
| 2 |
| 1 |
| 2 |
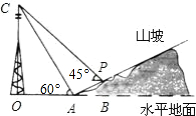 同一條直線上.求電視塔OC的高度以及此人所在位置點P的鉛直高度.(測傾器的高度忽略不計,結果保留根號形式)
同一條直線上.求電視塔OC的高度以及此人所在位置點P的鉛直高度.(測傾器的高度忽略不計,結果保留根號形式)查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
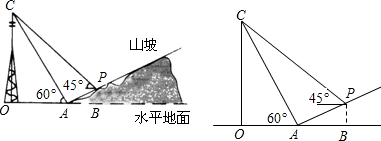
 如圖,某人在山坡坡腳A處測得電視塔尖點C的仰角為60°,沿山坡向上走到P處再測得點C的仰角為45°,已知OA=100米,該山坡的坡度為
如圖,某人在山坡坡腳A處測得電視塔尖點C的仰角為60°,沿山坡向上走到P處再測得點C的仰角為45°,已知OA=100米,該山坡的坡度為| 1 | 2 |
查看答案和解析>>
科目:初中數學 來源:2011-2012學年江蘇鎮江九年級5月中考模擬數學試卷(解析版) 題型:解答題
如圖,某人在山坡坡腳 處測得電視塔尖點
處測得電視塔尖點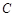 的仰角為
的仰角為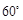 ,沿山坡向上走到
,沿山坡向上走到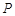 處再測得點
處再測得點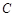 的仰角為
的仰角為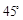 ,已知
,已知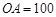 米,山坡坡度
米,山坡坡度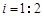 且O 、A、B在同一條直線上.求電視塔
且O 、A、B在同一條直線上.求電視塔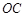 的高度以及此人所在位置點
的高度以及此人所在位置點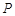 的鉛直高度.(測傾器高度忽略不計,結果保留根號形式)
的鉛直高度.(測傾器高度忽略不計,結果保留根號形式)

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com