
【題目】某加油站五月份營銷一種油品的銷售利潤![]() (萬元)與銷售量
(萬元)與銷售量![]() (萬升)之間函數關系的圖象如圖中折線所示,該加油站截止到13日調價時的銷售利潤為4萬元,截止至15日進油時的銷售利潤為5.5萬元.(銷售利潤=(售價-成本價)×銷售量)
(萬升)之間函數關系的圖象如圖中折線所示,該加油站截止到13日調價時的銷售利潤為4萬元,截止至15日進油時的銷售利潤為5.5萬元.(銷售利潤=(售價-成本價)×銷售量)
請你根據圖象及加油站五月份該油品的所有銷售記錄提供的信息,解答下列問題:

(1)求銷售量![]() 為多少時,銷售利潤為4萬元;
為多少時,銷售利潤為4萬元;
(2)分別求出線段AB與BC所對應的函數關系式;
(3)我們把銷售每升油所獲得的利潤稱為利潤率,那么,在OA、AB、BC三段所表示的銷售信息中,哪一段的利潤率最大?(直接寫出答案)
【答案】(1)4萬升;(2)線段![]() 所對應的函數關系式為
所對應的函數關系式為![]() ;線段
;線段![]() 所對應的函數關系式為
所對應的函數關系式為![]() ;(3)線段
;(3)線段![]() .
.
【解析】
(1)由題意可知,13日調價前,每升銷售利潤為1元,而在13日調價前銷售利潤剛好為4萬元,由此可得銷售利潤為4萬元時,銷售量為4÷1=4(萬升);
(2)由(1)可得點A的坐標為(4,4),根據題意結合圖形中的信息求出點B和點C的坐標,再用待定系數法即可求得線段AB與BC所對應的函數關系式;
(3)函數圖象從左至右上升越快,利潤隨銷售量的變化而變化的量越大,即利潤率就越大,由此可得AB段的利潤率最大.
(1)根據題意,當銷售利潤為4萬元,銷售量為![]() (萬升).
(萬升).
答:銷售量![]() 為4萬升時銷售利潤為4萬元.
為4萬升時銷售利潤為4萬元.
(2)由(1)可知點![]() 的坐標為
的坐標為![]() ,
,
∵從13日到15日利潤為![]() (萬元),
(萬元),
∴13日到15日的銷售量為![]() (萬升),
(萬升),
∴點![]() 的坐標為
的坐標為![]() .
.
設線段![]() 所對應的函數關系式為
所對應的函數關系式為![]() ,則
,則![]() ,解得
,解得![]() ,
,
∴ 線段![]() 所對應的函數關系式為
所對應的函數關系式為![]() .
.
∵從15日到31日銷售5萬升,利潤為![]() (萬元).
(萬元).
∴本月銷售該油品的利潤為![]() (萬元),
(萬元),
∴點![]() 的坐標為
的坐標為![]() .
.
設線段![]() 所對應的函數關系式為
所對應的函數關系式為![]() ,則
,則![]() 解得
解得![]()
∴線段![]() 所對應的函數關系式為
所對應的函數關系式為![]() .
.
(3)∵當函數圖象從左至由上升越快時,利潤隨銷售量的變化而變化的量就越大,即利潤率就越大,
∴結合圖形可得AB段的利潤率最大.


科目:初中數學 來源: 題型:
【題目】對于平面直角坐標系中的點![]() ,若點
,若點![]() 的坐標為
的坐標為![]() (其中
(其中![]() 為常數,且
為常數,且![]() )則稱點
)則稱點![]() 為點
為點![]() 的“
的“![]() 系雅培點”;
系雅培點”;
例如:![]() 的“3系雅培點”為
的“3系雅培點”為![]() ,即
,即![]() .
.
(1)點![]() 的“2系雅培點”
的“2系雅培點”![]() 的坐標為 ;
的坐標為 ;
(2)若點![]() 在
在![]() 軸的正半軸上,點
軸的正半軸上,點![]() 的“
的“![]() 系雅培點”為
系雅培點”為![]() 點,若在△
點,若在△![]() 中,
中,![]() ,求
,求![]() 的值;
的值;
(3)已知點![]() 在第四象限,且滿足
在第四象限,且滿足![]() ;點
;點![]() 是點
是點![]() 的“
的“![]() 系雅培點”,若分式方程
系雅培點”,若分式方程![]() 無解,求
無解,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某品牌汽車公司銷售部為了制定下個月的銷售計劃,對 20 位銷售員本月的銷售量進行了 統計,繪制成如圖所示的統計圖,則這 20 位銷售人員本月銷售量的平均數、中位數、眾數 分別是(單位:輛)( )

A.18.4,16,16B.18.4,20,16
C.19, 16,16D.19, 20,16
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某數學興趣小組要測量一棟五層居民樓CD的高度,該樓底層為車庫,高2.5米;上面五層居住,每層高度相等,測角儀支架離地1.5米,在A處測得五樓頂部點D的仰角為60°,在B處測得四樓頂部點E的仰角為30°,AB=14米,求居民樓的高度.(精確到0.1米,參考數據:![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 中,
中,![]() ,若動點
,若動點![]() 從點
從點![]() 開始,按
開始,按![]() 的路徑運動,且速度為每秒
的路徑運動,且速度為每秒![]() ,設出發的時間為
,設出發的時間為![]() 秒.
秒.

(1)當![]() 為幾秒時,
為幾秒時,![]() 平分
平分![]() ;
;
(2)問![]() 為何值時,
為何值時,![]() 為等腰三角形?
為等腰三角形?
(3)另有一點![]() ,從點
,從點![]() 開始,按
開始,按![]() 的路徑運動,且速度為每秒
的路徑運動,且速度為每秒![]() ,若
,若![]() 兩點同時出發,當
兩點同時出發,當![]() 中有一點到達終點時,另一點也停止運動. 當
中有一點到達終點時,另一點也停止運動. 當![]() 為何值時,直線
為何值時,直線![]() 把
把![]() 的周長分成相等的兩部分?
的周長分成相等的兩部分?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知點A(﹣4,0)、B(0,3),對△AOB連續作旋轉變換依次得到三角形(1)、(2)、(3)、(4)、…,則第(5)個三角形的直角頂點的坐標是_____,第(2018)個三角形的直角頂點的坐標是______.
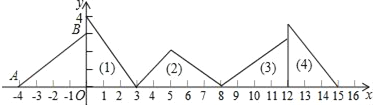
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】空中纜車是旅游時上山和進行空中參觀的交通工具,小明一家去某著名風景區旅游,準備先從山腳B走臺階步行到A,再換乘纜車到山項頂D.從B到A的路線可看作是坡角為50°的斜坡,長度為3000米;從A到D的纜車路線可看作直線,與水平線的夾角為30°,且纜車從A到D的平均速度為6m/s,時間為10分鐘,求山頂D的高度,(參考數據:sin50°≈0.77,cos50°≈0.64,tan50°≈1.2)
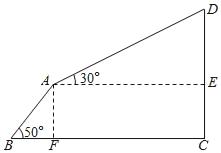
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,點B的坐標是(0,2),動點A從原點O出發,沿著x軸正方向移動,△ABP是以AB為斜邊的等腰直角三角形(點A、B、P順時針方向排列),當點A與原點O重合時,得到等腰直角△OBC(此時點P與點C重合).
(1)BC=______;當OA=2時,點P的坐標是______;
(2)設動點A的坐標為(t,0)(t≥0).
①求證:點A在移動過程中,△ABP的頂點P一定在射線OC上;
②用含t的代數式表示點P的坐標為:(______,______);
(3)過點P做y軸的垂線PQ,Q為垂足,當t=______時,△PQB與△PCB全等.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com