
【題目】某校開展“陽光體育”活動,決定開設乒乓球、籃球、跑步、跳繩這四種運動項目,學生只能選擇其中一種,為了解學生喜歡哪一種項目,隨機抽取了部分學生進行調查,并將調查結果繪制成兩張不完整的統計圖,請你結合圖中的信息解答下列問題:
(1)樣本中喜歡籃球項目的人數百分比是 ;其所在扇形統計圖中的圓心角的度數是 ;
(2)把條形統計圖補畫完整并注明人數;
(3)已知該校有1000名學生,根據樣本估計全校喜歡乒乓球的人數是多少?

【答案】(1)20%,72°;(2)答案見解析;(3)440.
【解析】試題分析:(1)利用1減去其它各組所占的比例即可求得喜歡籃球的人數百分比,利用百分比乘以360度即可求得扇形的圓心角的度數;
(2)根據喜歡A乒乓球的有44人,占44%即可求得調查的總人數,乘以對應的百分比即可求得喜歡籃球的人數,作出統計圖;
(3)總人數1000乘以喜歡乒乓球的人數所占的百分比即可求解.
試題解析:解:(1)1﹣44%﹣8%﹣28%=20%,所在扇形統計圖中的圓心角的度數是:360×20%=72°.故答案為:20%,72°;
(2)調查的總人數是:44÷44%=100(人),則喜歡籃球的人數是:100×20%=20(人),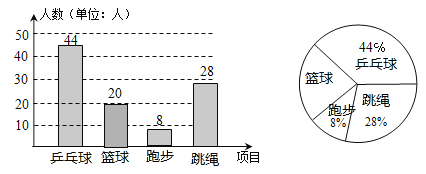 ;
;
(3)全校喜歡乒乓球的人數是1000×44%=440(人).
答:根據樣本估計全校喜歡乒乓球的人數是440人.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】如圖,旗桿AB的頂端B在夕陽的余輝下落在一個斜坡上的點D處,某校數學課外興趣小組的同學正在測量旗桿的高度,在旗桿的底部A處測得點D的仰角為15°,AC=10米,又測得∠BDA=45°.已知斜坡CD的坡度為i=1:![]() ,求旗桿AB的高度(
,求旗桿AB的高度(![]() ≈1.7,結果精確到個位).
≈1.7,結果精確到個位).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在平面直角坐標系中,已知A(2,2)、B(﹣2,0)、C(﹣1,﹣2).

(1)在平面直角坐標系中畫出△ABC;
(2)若點D與點C關于y軸對稱,則點D的坐標為 ;
(3)求△ABC的面積;
(4)已知點P為x軸上一點,若S△ABP=5時,求點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為提升硬件設施,決定采購80臺電腦,現有A,B兩種型號的電腦可供選擇.已知每臺A型電腦比B型的貴2000元,2臺A型電腦與3臺B型電腦共需24000元.
(1)分別求A,B兩種型號電腦的單價;
(2)若A,B兩種型號電腦的采購總價不高于38萬元,則A型電腦最多采購多少臺?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,四邊形OABC的頂點A在x軸上;∠COA=∠B=60°,且CB∥OA.
(1)求證,四邊形OABC是平行四邊形.
(2)若A的坐標為(8,0),OC長為6,求點B的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知△ABC中,AC=6cm,BC=8cm,AB=10cm,CD為AB邊上的高.動點P從點A出發,沿著△ABC的三條邊逆時針走一圈回到A點,速度為2cm/s,設運動時間為t s.
(1)求CD的長;
(2)t為何值時,△ACP是等腰三角形?
(3)若M為BC上一動點,N為AB上一動點,是否存在M,N使得AM+MN 的值最小?如果有,請直接寫出最小值,如果沒有,請說明理由。



查看答案和解析>>
科目:初中數學 來源: 題型:
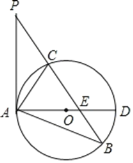
【題目】如圖,已知在![]() 中,C是BP邊上一點,PA是
中,C是BP邊上一點,PA是![]() 的切線,
的切線,![]() 是
是![]() 的外接圓,AD是
的外接圓,AD是![]() 的直徑,且交BP于點E.
的直徑,且交BP于點E.
![]() 求證:
求證:![]() ;
;
![]() 過點C作
過點C作![]() ,垂足為點F,延長CF交AB于點G,若
,垂足為點F,延長CF交AB于點G,若![]() ,AF:
,AF:![]() :3,
:3,![]()
①求CF的長;
②求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了保護環境,某企業決定購買10臺污水處理設備;現有A、B兩種型號的設備,其中每臺的價格、月處理污水量及年消耗費如下表:
A型 | B型 | |
價格(萬元/臺) | 12 | 10 |
處理污水量(噸/月) | 240 | 200 |
年消耗費(萬元/臺) | 1 | 1 |
經預算,該企業購買設備的資金不高于105萬元。
(1) 請你設計該企業有幾種購買方案;
(2)若該企業每月產生的污水量為2040噸,為了節約資金,應選擇哪種購買方案?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com