
【題目】如圖,在平面直角坐標系中,一次函數y=kx+b(k≠0)的圖象與反比例函數y= ![]() (m≠0)的圖象交于A、B兩點,與x軸交于C點,點A的坐標為(n,6),點C的坐標為(﹣2,0),且tan∠ACO=2.
(m≠0)的圖象交于A、B兩點,與x軸交于C點,點A的坐標為(n,6),點C的坐標為(﹣2,0),且tan∠ACO=2. 
(1)求該反比例函數和一次函數的解析式;
(2)求點B的坐標.
【答案】
(1)解:過點A作AD⊥x軸,垂足為D

由A(n,6),C(﹣2,0)可得,
OD=n,AD=6,CO=2
∵tan∠ACO=2
∴ ![]() =2,即
=2,即 ![]() =2
=2
∴n=1
∴A(1,6)
將A(1,6)代入反比例函數,得m=1×6=6
∴反比例函數的解析式為 ![]()
將A(1,6),C(﹣2,0)代入一次函數y=kx+b,可得
![]()
解得 ![]()
∴一次函數的解析式為y=2x+4
(2)解:由  可得
可得 ![]()
![]()
解得x1=1,x2=﹣3
∵當x=﹣3時,y=﹣2
∴點B坐標為(﹣3,﹣2)
【解析】本題主要考查了反比例函數與一次函數的交點問題,解決問題的關鍵是掌握待定系數法求函數解析式.求反比例函數與一次函數的交點坐標時,把兩個函數關系式聯立成方程組求解,若方程組有解,則兩者有交點,若方程組無解,則兩者無交點.(1)先過點A作AD⊥x軸,根據tan∠ACO=2,求得點A的坐標,進而根據待定系數法計算兩個函數解析式;(2)先聯立兩個函數解析式,再通過解方程求得交點B的坐標即可.


科目:初中數學 來源: 題型:
【題目】解不等式組: .
.
請結合題意,完成本題的解答.
(1)解不等式①,得 ,依據是: .
(2)解不等式③,得 .
(3)把不等式①,②和③的解集在數軸上表示出來.
![]()
(4)從圖中可以找出三個不等式解集的公共部分,得不等式組的解集 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD的對角線AC、BD交于點O,且DE∥AC,CE∥BD.
(1)求證:四邊形OCED是菱形;
(2)若∠BAC=30°,AC=4,求菱形OCED的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
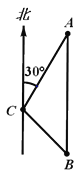
【題目】如圖,一艘輪船位于燈塔C的北偏東30°方向上的A處,且A處距離燈塔C處80海里,輪船沿正南方向勻速航行一段時間后,到達位于燈塔C的東南方向上的B處.
(1)求燈塔C到達航線AB的距離;
(2)若輪船的速度為20海里/時,求輪船從A處到B處所用的時間(結果保留根號).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,一次函數y=ax+b的圖象與反比例函數y=![]() 的圖象交于一、三象限內的A、B兩點,與x軸交于C點,點A的坐標為(2,m),點B的坐標為(n,﹣2),tan∠BOC=
的圖象交于一、三象限內的A、B兩點,與x軸交于C點,點A的坐標為(2,m),點B的坐標為(n,﹣2),tan∠BOC=![]() .
.
(1)求該反比例函數和一次函數的解析式.
(2)求△BOC的面積.
(3)P是x軸上的點,且△PAC的面積與△BOC的面積相等,求P點的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,一次函數y=ax+b(a≠0)的圖形與反比例函數y= ![]() (k≠0)的圖象交于第二、四象限內的A、B兩點,與y軸交于C點,過點A作AH⊥y軸,垂足為H,OH=3,tan∠AOH=
(k≠0)的圖象交于第二、四象限內的A、B兩點,與y軸交于C點,過點A作AH⊥y軸,垂足為H,OH=3,tan∠AOH= ![]() ,點B的坐標為(m,﹣2).
,點B的坐標為(m,﹣2). 
(1)求△AHO的周長;
(2)求該反比例函數和一次函數的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“校園安全”受到社會的廣泛關注,某校政教處對部分學生就校園安全知識的了解程度,進行了隨機抽樣調查,并繪制了如下兩幅尚不完整的統計圖.請你根據統計圖中所提供的信息解答下列問題:
(1)接受問卷調查的學生共有______名;
(2)請補全折線統計圖,并求出扇形統計圖中“基本了解”部分所對應扇形的圓心角的大小.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:在平面直角坐標系中,![]() 、
、![]() 兩點的坐標分別為
兩點的坐標分別為![]() 、
、![]() ,
,![]() 、
、![]() 分別是
分別是![]() 軸、
軸、![]() 軸上的點.如果以點
軸上的點.如果以點![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的四邊形是平行四邊形,則
為頂點的四邊形是平行四邊形,則![]() 的坐標為__________.
的坐標為__________.
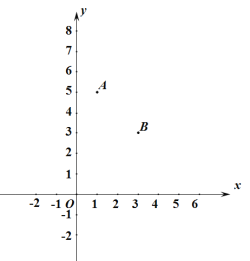
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,點A(![]() ,0),AB⊥
,0),AB⊥![]() 軸,且AB=10,點C(0,b),
軸,且AB=10,點C(0,b),![]() ,b滿足
,b滿足![]() .點P(t,0)是線段AO上一點(不包含A,O)
.點P(t,0)是線段AO上一點(不包含A,O)
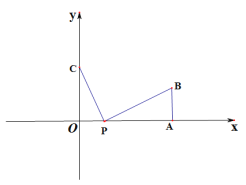
(1)當t=5時,求PB:PC的值;
(2)當PC+PB最小時,求t的值;
(3)請根據以上的啟發,解決如下問題:正數m,n滿足m+n=10,且正數![]() =
=![]() ,則正數
,則正數![]() 的最小值=________.
的最小值=________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com