
【題目】我市部分學生參加了全國初中數學競賽決賽,并取得優異成績.已知競賽成績分數都是整數,試題滿分為140分,參賽學生的成績分數分布情況如下:
分數段 | 0-19 | 20-39 | 40-59 | 60-79 | 80-99 | 100-119 | 120-140 |
人數 | 0 | 37 | 68 | 95 | 56 | 32 | 12 |
請根據以上信息解答下列問題:
(1)全市共有多少人參加本次數學競賽決賽?最低分和最高分在什么分數范圍?
(2)經競賽組委會評定,競賽成績在60分以上(含60分)的考生均可獲得不同等級的獎勵,求我市參加本次競賽決賽考生的獲獎比例;
(3)決賽成績分數的中位數落在哪個分數段內?
(4)上表還提供了其他信息,例如:“沒獲獎的人數為105人”等等.請你再寫出兩條此表提供的信息.
【答案】(1)全市共有300名學生參加本次競賽決賽,最低分在20-39之間,最高分在120-140之間;(2)65%;(3)中位數落在60-79分數段內;(4)如“120分以上有12人;60至79分數段的人數最多”等,答案不唯一.
【解析】
(1)把圖表中的人數加起來即可;
(2)60分以上的人數有195人,用195除以總人數得獲獎率;
(3)由中位數概念判斷;
(4)答案不唯一,寫出正確信息即可.
解:(1)37+68+95+56+32+12=300,即全市共有300名學生參加本次競賽決賽,最低分在20-39之間,最高分在120-140之間;
(2)60分以上的人數有95+56+32+12=195人,則本次決賽共有195人獲獎,獲獎率為![]() ×100%=65%;
×100%=65%;
(3)將這組數據按從小到大排列為,由于有偶數個數,取最中間兩個數的平均數,第150、151位都是60-79分數段內,則決賽成績的中位數落在60-79分數段內;
(4)如“120分以上有12人;60至79分數段的人數最多”等.


科目:初中數學 來源: 題型:
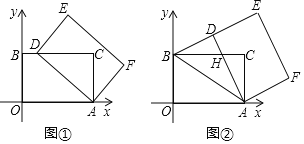
【題目】在平面直角坐標系中,四邊形AOBC是矩形,點O(0,0),點A(5,0),點B(0,3).以點A為中心,順時針旋轉矩形AOBC,得到矩形ADEF,點O,B,C的對應點分別為D,E,F.
(1)如圖①,當點D落在BC邊上時,求點D的坐標;
(2)如圖②,當點D落在線段BE上時,AD與BC交于點H.
①求證△ADB≌△AOB;
②求點H的坐標.
(3)記K為矩形AOBC對角線的交點,S為△KDE的面積,求S的取值范圍(直接寫出結果即可).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示是一塊含30°,60°,90°的直角三角板,直角頂點O位于坐標原點,斜邊AB垂直x軸,頂點A在函數y1=![]() (x>0)的圖象上,頂點B在函數y2=
(x>0)的圖象上,頂點B在函數y2=![]() (x>0)的圖象上,∠ABO=30°,則
(x>0)的圖象上,∠ABO=30°,則![]() =( )
=( )

A. ﹣![]() B. ﹣
B. ﹣![]() C. ﹣
C. ﹣![]() D. ﹣
D. ﹣![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,OA和OB是⊙O的半徑,OB=2,OA⊥OB,P是OA上任一點,BP的延長線交⊙O于點Q,過點Q的⊙O的切線交OA延長線于點R.
(1)求證:RP=RQ;
(2)若OP=PQ,求PQ的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】拋物線![]() 與
與![]() 軸交于A、B兩點,點P在函數
軸交于A、B兩點,點P在函數![]() 的圖象上,若△PAB為直角三角形,則滿足條件的點P的個數為( ).
的圖象上,若△PAB為直角三角形,則滿足條件的點P的個數為( ).
A. 2個 B. 3個 C. 4個 D. 6個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知直線l經過A(6,0)和B(0,12)兩點,且與直線y=x交于點C,點P(m,0)在x軸上運動.
(1)求直線l的解析式;
(2)過點P作l的平行線交直線y=x于點D,當m=3時,求△PCD的面積;
(3)是否存在點P,使得△PCA成為等腰三角形?若存在,請直接寫出所有符合條件的點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
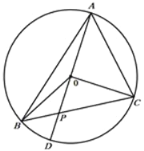
【題目】如圖,△ABC內接于圓O,∠BOC=120°,AD為圓O的直徑.AD交BC于P點且PB=1,PC=2,則AC的長為( )
A. ![]() B.
B. ![]() C. 3D. 2
C. 3D. 2![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
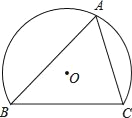
【題目】如圖,弓形ABC中,∠BAC=60°,BC=2![]() ,若點P在優弧BAC上由點B向點C移動,記△PBC的內心為I,點I隨點P的移動所經過的路程為m,則m的取值范圍為_____.
,若點P在優弧BAC上由點B向點C移動,記△PBC的內心為I,點I隨點P的移動所經過的路程為m,則m的取值范圍為_____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com