
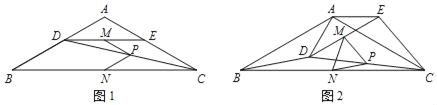
【題目】如圖1,在△ABC中,AB=AC,∠BAC=120°,點D,E分別在邊AB,AC上,AD=AE,連接DC,點M,P,N分別為DE,DC,BC的中點.
(1)觀察猜想
圖1中,線段PM與PN的數量關系是 ,∠MPN的度數是 ;
(2)探究證明
把△ADE繞點A逆時針方向旋轉到圖2的位置,連接MN,BD,CE,判斷△PMN的形狀,并說明理由;
(3)拓展延伸
把△ADE繞點A在平面內自由旋轉,若AD=4,AB=8,請直接寫出△PMN面積的取值范圍.
【答案】(1)PM=PN,60°;(2)詳見解析;(3)![]() ≤S△PMN≤9
≤S△PMN≤9![]() .
.
【解析】
(1)利用三角形的中位線得出PM=![]() CE,PN=
CE,PN=![]() BD,進而判斷出BD=CE,即可得出結論,再利用三角形的中位線得出PM∥CE得出∠DPM=∠DCA,最后用互余即可得出結論;
BD,進而判斷出BD=CE,即可得出結論,再利用三角形的中位線得出PM∥CE得出∠DPM=∠DCA,最后用互余即可得出結論;
(2)先判斷出△ABD≌△ACE,得出BD=CE,同(1)的方法得出PM=![]() BD,PN=
BD,PN=![]() BD,即可得出PM=PN,同(1)的方法即可得出結論;
BD,即可得出PM=PN,同(1)的方法即可得出結論;
(3)先判斷出BD最大時,△PMN的面積最大,而BD最大是AB+AD=12,再判斷出BD最小時,△PMN最小,即可得出結論.
解:(1)∵點P,N是BC,CD的中點,
∴PN∥BD,PN=![]() BD,
BD,
∵點P,M是CD,DE的中點,
∴PM∥CE,PM=![]() CE,
CE,
∵AB=AC,AD=AE,
∴BD=CE,
∴PM=PN,
∵PN∥BD,
∴∠DPN=∠ADC,
∵PM∥CE,
∴∠DPM=∠DCA,
∵∠BAC=120°,
∴∠ADC+∠ACD=60°,
∴∠MPN=∠DPM+∠DPN=∠DCA+∠ADC=60°,
故答案為:PM=PN,60°;
(2)△PMN是等腰直角三角形.
由旋轉知,∠BAD=∠CAE,
∵AB=AC,AD=AE,
∴△ABD≌△ACE(SAS),
∴∠ABD=∠ACE,BD=CE,
利用三角形的中位線得,PN=BD,PM=![]() CE,
CE,
∴PM=PN,
∴△PMN是等腰三角形,
同(1)的方法得,PM∥CE,
∴∠DPM=∠DCE,
同(1)的方法得,PN∥BD,
∴∠PNC=∠DBC,
∵∠DPN=∠DCB+∠PNC=∠DCB+∠DBC,
∴∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC
=∠BCE+∠DBC=∠ACB+∠ACE+∠DBC
=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC,
∵∠BAC=120°,
∴∠ACB+∠ABC=60°,
∴∠MPN=60°,
∴△PMN是等邊三角形;
(3)由(2)知,△PMN是等邊三角形,PM=PN=![]() BD,
BD,
∴PM最大時,△PMN面積最大,PM最小時,△PMN面積最小
∴點D在BA的延長線上,△PMN的面積最大,
∴BD=AB+AD=12,
∴PM=6,
∴S△PMN最大=![]() PM2=
PM2=![]() ×62=9
×62=9![]() ,
,
當點D在線段AB上時,△PMN的面積最小,
∴BD=AB﹣AD=4,
∴PM=2,
S△PMN最小=![]() PM2=
PM2=![]() ×22=
×22=![]() ,
,
∴![]() ≤S△PMN≤9
≤S△PMN≤9![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】如圖,把平面內一條數軸x繞點O逆時針旋轉角θ(0°<θ<90°)得到另一條數軸y,x軸和y軸構成一個平面斜坐標系.規定:已知點P是平面斜坐標系中任意一點,過點P作y軸的平行線交x軸于點A,過點P作x軸的平行線交y軸于點B,若點A在x軸上對應的實數為a,點B在y軸上對應的實數為b,則稱有序實數對(a,b)為點P的斜坐標.在平面斜坐標系中,若θ=45°,點P的斜坐標為(1,2![]() ),點G的斜坐標為(7,﹣2
),點G的斜坐標為(7,﹣2![]() ),連接PG,則線段PG的長度是_____.
),連接PG,則線段PG的長度是_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
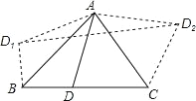
【題目】如圖,在△ABC中,∠ABC=45°,∠ACB=60°,BC=2![]() +2,D是BC邊上異于點B,C的一動點,將三角形ABD沿AB翻折得到△ABD1,將△ACD沿AC翻折得到△ACD2,連接D1D2,則四邊形D1BCD2的面積的最大值是_____.
+2,D是BC邊上異于點B,C的一動點,將三角形ABD沿AB翻折得到△ABD1,將△ACD沿AC翻折得到△ACD2,連接D1D2,則四邊形D1BCD2的面積的最大值是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知矩形OABC中,OA=3,AB=4,雙曲線![]() (k>0)與矩形兩邊AB、BC分別交于D、E,且BD=2AD
(k>0)與矩形兩邊AB、BC分別交于D、E,且BD=2AD
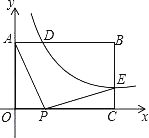
(1)求k的值和點E的坐標;
(2)點P是線段OC上的一個動點,是否存在點P,使∠APE=90°?若存在,求出此時點P的坐標,若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】《九章算術》是我國古代第一部自成體系的數學專著,代表了東方數學的最高成就.它的算法體系至今仍在推動著計算機的發展和應用.書中記載:“今有圓材埋在壁中,不知大小,以鋸鋸之,深一寸,鋸道長一尺,問徑幾何?”譯為:“今有一圓柱形木材,埋在墻壁中,不知其大小,用鋸去鋸這木材,鋸口深1寸(ED=1寸),鋸道長1尺(AB=1尺=10寸)”,問這塊圓形木材的直徑是多少?”
如圖所示,請根據所學知識計算:圓形木材的直徑AC是( )
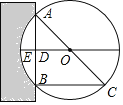
A. 13寸 B. 20寸 C. 26寸 D. 28寸
查看答案和解析>>
科目:初中數學 來源: 題型:
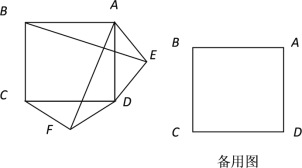
【題目】如圖,在正方形ABCD的外側, 作兩個等腰三角形ADE和DCF,
(1) 若EA=ED=FD=FC,請判斷BE和AF的關系?并給予證明.
(2)若三角形ADE和DCF為一般三角形,且AE=DF,ED=FC,請用備用圖畫出圖形,直接寫出BE和AF的關系,不用證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,對角線AC的垂直平分線EF分別交AD、AC、BC于點E、O、F,連接CE和AF.
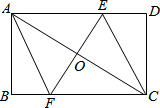
(1)求證:四邊形AECF為菱形;
(2)若AB=4,BC=8,求菱形AECF的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形紙片ABCD中,AB=4,BC=8,將紙片沿EF折疊,使點C與點A重合,則下列結論錯誤的是( )
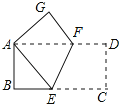
A.△ABE≌△AGFB.AE=AFC.AE=EFD.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com