
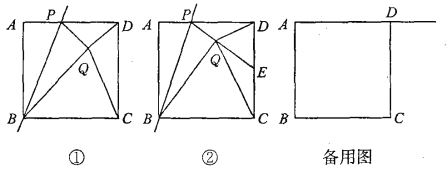
【題目】如圖①,已知正方形ABCD的邊長為1,點P是AD邊上的一個動點,點A關于直線BP的對稱點是點Q,連接PQ、DQ、CQ、BQ,設AP=x.
(1)BQ+DQ的最小值是_______,此時x的值是_______;
(2)如圖②,若PQ的延長線交CD邊于點E,并且∠CQD=90°.
①求證:點E是CD的中點; ②求x的值.
(3)若點P是射線AD上的一個動點,請直接寫出當△CDQ為等腰三角形時x的值.
【答案】(1)![]() ,
,![]() ;(2) ①理由詳見解析;②
;(2) ①理由詳見解析;②![]() ;(3) 2﹣
;(3) 2﹣![]() 或
或![]() 或2+
或2+![]() .
.
【解析】
試題分析:(1)根據兩點之間,線段最短可知,點Q在線段BD上時BQ+DQ的值最小,是BD的長度,利用勾股定理即可求出;再根據△PDQ是等腰直角三角形求出x的值;
(2) ①由對稱可知AB=BQ=BC,因此∠BCQ=∠BQC.根據∠BQE=∠BCE=90°,可知∠EQC=∠ECQ,從而EQ=EC.再根據∠CQD=90°可得∠DQE+∠CQE=90°, ∠QCE+∠QDE=90°,而∠EQC=∠ECQ, 所以∠QDE=∠DQE,從而EQ=ED.易得點E是CD的中點;②在Rt△PDE中,PE= PQ+QE=x+![]() ,PD=1﹣x,PQ=x,根據勾股定理即可求出x的值.
,PD=1﹣x,PQ=x,根據勾股定理即可求出x的值.
(3) △CDQ為等腰三角形分兩種情況:①CD為腰,以點C 為圓心,以CD的長為半徑畫弧,兩弧交點即為使得△CDQ為等腰三角形的Q點; ②CD為底邊時,作CD的垂直平分線,與![]() 的交點即為△CDQ為等腰三角形的Q點,則共有 3個Q點,那么也共有3個P點,作輔助線,利用直角三角形的性質求之即得.
的交點即為△CDQ為等腰三角形的Q點,則共有 3個Q點,那么也共有3個P點,作輔助線,利用直角三角形的性質求之即得.
試題解析:(1)![]() ,
,![]() .
.
(2)①證明:在正方形ABCD中,
AB=BC,∠A=∠BCD=90°.
∵Q點為A點關于BP的對稱點,
∴AB=QB,∠A=∠PQB=90°,
∴QB=BC,∠BQE=∠BCE,
∴∠BQC=∠BCQ,
∴∠EQC=∠EQB﹣∠CQB=∠ECB﹣∠QCB=∠ECQ,
∴EQ=EC.
在Rt△QDC中,
∵∠QDE=90°﹣∠QCE,
∠DQE=90°﹣∠EQC,
∴∠QDE=∠DQE,
∴EQ=ED,
∴CE=EQ=ED,即E為CD的中點.
②∵AP=x,AD=1,
∴PD=1﹣x,PQ=x,CD=1.
在Rt△DQC中,
∵E為CD的中點,
∴DE=QE=CE=![]() ,
,
∴PE=PQ+QE=x+![]() ,
,
∴![]() ,
,
解得 x=![]() .
.
(3)△CDQ為等腰三角形時x的值為2-![]() ,
,![]() ,2+
,2+![]() .
.
如圖,以點B為圓心,以AB的長為半徑畫弧,以點C為圓心,以CD的長為半徑畫弧,兩弧分別交于Q1,Q3.此時△CDQ1,△CDQ3都為以CD為腰的等腰三角形.作CD的垂直平分線交弧AC于點Q2,此時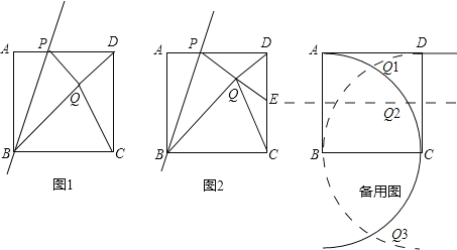
△CDQ2以CD為底的等腰三形.
以下對此Q1,Q2,Q3.分別討論各自的P點,并求AP的值.
討論Q:如圖作輔助線,連接BQ1、CQ1,作PQ1⊥BQ1交AD于P,過點Q1,作EF⊥AD于E,交BC于F.
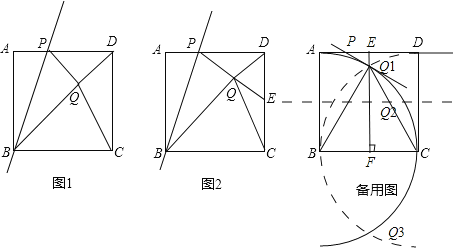
∵△BCQ1為等邊三角形,正方形ABCD邊長為1,
∴![]() ,
,![]() .
.
在四邊形ABPQ1中,
∵∠ABQ1=30°,
∴∠APQ1=150°,
∴△PEQ1為含30°的直角三角形,
∴PE=![]() .
.
∵AE=![]() ,
,
∴x=AP=AE-PE=2-![]() .
.
②討論Q2,如圖作輔助線,連接BQ2,AQ2,過點Q2作PG⊥BQ2,交AD于P,連接BP,過點Q2作EF⊥CD于E,交AB于F.

∵EF垂直平分CD,
∴EF垂直平分AB,
∴AQ2=BQ2.
∵AB=BQ2,
∴△ABQ2為等邊三角形.
在四邊形ABQP中,
∵∠BAD=∠BQP=90°, ∠ABQ=60°,
∴∠APE=120°
∴∠EQ2G=∠DPG=180°-120°=60°,
∴![]() ,
,
∴EG=![]() ,
,
∴DG=DE+GE=![]() -1,
-1,
∴PD=1-![]() ,
,
∴x=AP=1-PD=![]() .
.
③對Q3,如圖作輔助線,連接BQ1,CQ1,BQ3,CQ3,過點Q3作BQ3⊥PQ3,交AD的延長線于P,連接BP,過點Q1,作EF⊥AD于E,此時Q3在EF上,不妨記Q3與F重合.
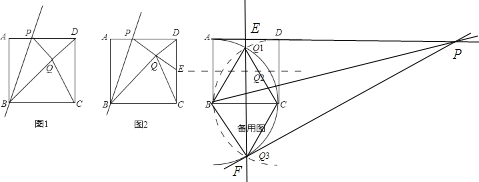
∵△BCQ1為等邊三角形,△BCQ3為等邊三角形,BC=1,
∴![]() ,
,![]() ,
,
∴![]() .
.
在四邊形ABQ3P中
∵∠ABF=∠ABC+∠CBQ3=150°,
∴∠EPF=30°,
∴EP=![]() ,EF=
,EF=![]() .
.
∵AE=![]() ,
,
∴x=AP=AE+PE=![]() +2.
+2.
綜上所述,△CDQ為等腰三角形時x的值為2﹣![]() ,
,![]() ,2+
,2+![]() .
.


科目:初中數學 來源: 題型:
【題目】為迎接安順市文明城市創建工作,某校八年一班開展了“社會主義核心價值觀、未成年人基本文明禮儀規范”的知識競賽活動,成績分為A、B、C、D四個等級,并將收集的數據繪制了兩幅不完整的統計圖.請你根據圖中所給出的信息,解答下列各題:
(1)求八年一班共有多少人;
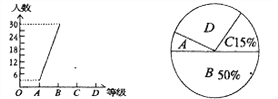
(2)補全折線統計圖;
(3)在扇形統計圖中等極為“D”的部分所占圓心角的度數為________;
(4)若等級A為優秀,求該班的優秀率.
【答案】(1)60;(2)補圖見解析;(3)108°;(4)5%.
【解析】(1)用B等人數除以其所占的百分比即可得到總人數;
(2)用求得的總人數乘以C等所占的百分比即可得到C等的人數,總人數減去A、C等的人數即可求得D等的人數;
(3)用D等的人數除以總人數乘以360°即可得到答案;
(4)用A等的人數除以總人數乘以100%即可得到答案. 解答:
解:(1)30÷50%=60(人)
∴八年級一共有60人。
(2)等級為“C”的人數為60×15%=9(人).
等級為“D”的人數為603309=18(人).
補全折線統計圖如下。
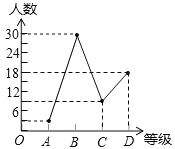
(3)等極為“D”的部分所占圓心角的度數為![]() ×360°=108°,
×360°=108°,
故答案為:108°.
(4)該班的優秀率![]() ×100%=5%.
×100%=5%.
∴該班的優秀率為5%.
點睛:本題考查統計相關知識.利用拆線圖與扇形圖得出相關信息是解題的關鍵.
【題型】解答題
【結束】
25
【題目】已知拋物線y=ax2+bx+c經過A(﹣1,0),B(3,0),C(0,3)三點,直線L是拋物線的對稱軸.
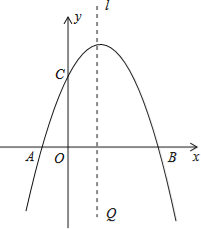
(1)求拋物線的函數關系式;
(2)求拋物線的頂點坐標;
(3)設P點是直線L上的一個動點,當△PAC的周長最小時,求點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
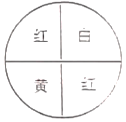
【題目】如圖,小華蒙上眼睛投飛鏢且中目標(轉盤技等分成4個扇形,投在邊線上忽略)(直接填寫答案)
(1)擊中紅色區域的概率是 .
(2)擊中白色區域的概率是 .
(3)沒有擊中黃色區域的概率是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了更好改善河流的水質,治污公司決定購買10臺污水處理設備![]() 現有A,B兩種型號的設備,其中每臺的價格,月處理污水量如下表:經調查:購買一臺A型設備比購買一臺B型設備多2萬元,購買2臺A型設備比購買3臺B型設備少6萬元.
現有A,B兩種型號的設備,其中每臺的價格,月處理污水量如下表:經調查:購買一臺A型設備比購買一臺B型設備多2萬元,購買2臺A型設備比購買3臺B型設備少6萬元.
A型 | B型 | |
價格 | a | b |
處理污水量 | 240 | 200 |
![]() 求a,b的值;
求a,b的值;
![]() 治污公司經預算購買污水處理設備的資金不超過105萬元,你認為該公司有哪幾種購買方案;
治污公司經預算購買污水處理設備的資金不超過105萬元,你認為該公司有哪幾種購買方案;
![]() 在
在![]() 的條件下,若每月要求處理污水量不低于2040噸,為了節約資金,請你為治污公司設計一種最省錢的購買方案.
的條件下,若每月要求處理污水量不低于2040噸,為了節約資金,請你為治污公司設計一種最省錢的購買方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知A(-4,![]() )、B(2,-4)是一次函數
)、B(2,-4)是一次函數![]() 的圖象和反比例函數
的圖象和反比例函數![]() 的圖象的兩個交點.
的圖象的兩個交點.
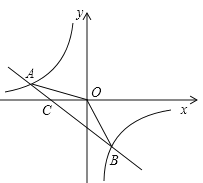
(1)求反比例函數和一次函數的解析式;
(2)求直線AB與![]() 軸的交點C的坐標及△AOB的面積;
軸的交點C的坐標及△AOB的面積;
(3)求方程![]() 的解(直接寫出答案)
的解(直接寫出答案)
(4)求不等式![]() 的解集(直接寫出答案)
的解集(直接寫出答案)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB為⊙O的直徑,點C為⊙O上一點,若∠BAC=∠CAM,過點C作直線l垂直于射線AM,垂足為點D.
(1)試判斷CD與⊙O的位置關系,并說明理由;
(2)若直線l與AB的延長線相交于點E,⊙O的半徑為3,并且∠CAB=30°,求CE的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解我市市民2018年乘坐公交車的每人月均花費情況,相關部門隨機調查了1000人的相關信息,并繪制了如圖所示的頻數直方圖,根據圖中提供的信息,有下列說法(每組值包括最低值,不包括最高值):①乘坐公交車的月均花費在60元~80元的人數最多;②月均花費在160元(含160元)以上的人數占所調查總人數的10%;③在所調查的1000人中,至少有一半以上的人的月均花費超過75元;④為了讓市民享受更多的優惠,相關部門擬確定一個折扣標準,計劃使30%左右的人獲得優惠,那么可以是乘坐公交車的月均花費達到100元(含100元)以上的人享受折扣.

A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點![]() 是∠
是∠![]() 內的一點,過點
內的一點,過點![]() 作
作![]() 于點
于點![]() 于點
于點![]() ,且
,且![]() .
.
![]() 求證:
求證: ![]() ;
;
![]() 如圖②,點
如圖②,點![]() 是射線
是射線![]() 上一點,點
上一點,點![]() 是線段
是線段![]() 上一點,且
上一點,且![]() ,若
,若![]() .求線段
.求線段![]() 的長.
的長.
![]() 如圖③,若
如圖③,若![]() ,將
,將![]() 繞點
繞點![]() 以每秒
以每秒![]() 的速度順時針旋轉,
的速度順時針旋轉,![]() 秒后,
秒后,![]() 開始繞點
開始繞點![]() 以每秒
以每秒![]() 的速度順時針旋轉,
的速度順時針旋轉,![]() 旋轉
旋轉![]() 后停止,此時
后停止,此時![]() 也隨之停止旋轉。旋轉過程中,
也隨之停止旋轉。旋轉過程中,![]() 所在直線與
所在直線與![]() 所在直線的交點記為
所在直線的交點記為![]() 所在直線與
所在直線與![]() 所在直線的交點記為
所在直線的交點記為![]() .問
.問![]() 旋轉幾秒時,
旋轉幾秒時,![]() ?
?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,“和諧號”高鐵列車的小桌板收起時,小桌板的支架底端與桌面頂端的距離OA=75厘米,且可以近似看作與地面垂直.展開小桌板使桌面保持水平,此時CB⊥AO,∠AOB=∠ACB=37°,且支架長OB與桌面寬BC的長度之和等于OA的長度.求小桌板桌面的寬度BC.(參考數據![]() ,
, ![]() ,
, ![]() )
)

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com