
【題目】如圖,已知二次函數![]() 的圖象經過
的圖象經過![]() 三點.
三點.
(1)求該二次函數的解析式;
(2)點![]() 是該二次函數圖象上的一點,且滿足
是該二次函數圖象上的一點,且滿足![]() (
(![]() 是坐標原點),求點
是坐標原點),求點![]() 的坐標;
的坐標;
(3)點![]() 是該二次函數圖象上位于一象限上的一動點,連接
是該二次函數圖象上位于一象限上的一動點,連接![]() 分別交
分別交![]() 軸與點
軸與點![]() 若
若![]() 的面積分別為
的面積分別為![]() 求
求![]() 的最大值.
的最大值.

【答案】(1)![]() ;(2)滿足條件的點
;(2)滿足條件的點![]() 有:
有:![]()
![]() ;(3)當
;(3)當![]() 時,
時,![]() 有最大值,最大值為:
有最大值,最大值為:![]() .
.
【解析】
試題分析:(1)利用待定系數法求得二次函數的解析式即可;(2)設![]() 直線與
直線與![]() 軸的交點為
軸的交點為![]() ,根據已知條件求得t=±8,根據t的值求得直線BD的解析式,把直線BD的解析式與拋物線的解析式聯立組成方程組,解方程組即可求得點D的坐標;(3)過點P作PH//
,根據已知條件求得t=±8,根據t的值求得直線BD的解析式,把直線BD的解析式與拋物線的解析式聯立組成方程組,解方程組即可求得點D的坐標;(3)過點P作PH//![]() 軸交
軸交![]() 直線于點
直線于點![]() ,設
,設![]() ,則
,則![]() ,所以
,所以![]() ,分別用t表示出
,分別用t表示出![]() 的面積分別為
的面積分別為![]() 在計算出
在計算出![]() 與t的函數關系,利用二次函數的性質求解即可.=
與t的函數關系,利用二次函數的性質求解即可.=
試題解析:
(1)由題意得:設拋物線的解析式為:![]() ;
;
因為拋物線圖像過點![]() ,
,
![]() 解得
解得![]()
所以拋物線的解析式為:![]()
即:![]()
(2)設![]() 直線與
直線與![]() 軸的交點為
軸的交點為![]()

當![]() 時,直線
時,直線![]() 解析式為:
解析式為:![]()
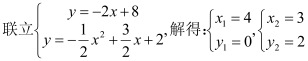
所以,點![]()
當![]() 時,直線
時,直線![]() 解析式為:
解析式為:![]()

所以,點![]()
綜上:滿足條件的點![]() 有:
有:![]()
![]()
(3):過點P作PH//![]() 軸交
軸交![]() 直線于點
直線于點![]() ,設
,設![]()
BC直線的解析式為![]() 故:
故:![]()
![]()
AP直線的解析式為:![]()
故:![]()

![]() ;
;
![]()
![]()
即:![]()
所以,當![]() 時,
時,![]() 有最大值,最大值為:
有最大值,最大值為:![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】為籌備班級的初中聯歡會,班委會經過討論決定在蘋果、桔子、香蕉、梨四種水管中選出一種購買,班長對全班學生愛吃那種水果做了調查,則最終在決定購買哪種水果時,下面的調查數據最值得關注的是( )
A.眾數B.平均數C.中位數D.方差
查看答案和解析>>
科目:初中數學 來源: 題型:
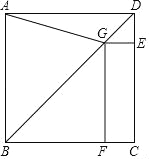
【題目】如圖,在正方形ABCD中,點G在對角線BD上(不與點B,D重合),GE⊥DC于點E,GF⊥BC于點F,連結AG.
(1)寫出線段AG,GE,GF長度之間的數量關系,并說明理由;
(2)若正方形ABCD的邊長為1,∠AGF=105°,求線段BG的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com