
【題目】已知拋物線![]() 與y軸交于點C,與x軸的兩個交點分別為A(﹣4,0),B(1,0).
與y軸交于點C,與x軸的兩個交點分別為A(﹣4,0),B(1,0).
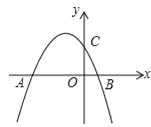
(1)求拋物線的解析式;
(2)已知點P在拋物線上,連接PC,PB,若△PBC是以BC為直角邊的直角三角形,求點P的坐標;
(3)已知點E在x軸上,點F在拋物線上,是否存在以A,C,E,F為頂點的四邊形是平行四邊形?若存在,請直接寫出點E的坐標;若不存在,請說明理由.
【答案】(1)![]() ;(2)滿足條件的P點坐標為(﹣4,0),P2(﹣5,﹣3);
;(2)滿足條件的P點坐標為(﹣4,0),P2(﹣5,﹣3);
(3)E為(﹣7,0)或(﹣1,0)或(![]() ,﹣2)或(
,﹣2)或(![]() ,﹣2).
,﹣2).
【解析】
試題分析:(1)因為拋物線經過點A(﹣4,0),B(1,0),所以可以設拋物線為y=﹣![]() (x+4)(x﹣1),展開即可解決問題.
(x+4)(x﹣1),展開即可解決問題.
(2)先證明∠ACB=90°,點A就是所求的點P,求出直線AC解析式,再求出過點B平行AC的直線的解析式,利用方程組即可解決問題.
(3)分AC為平行四邊形的邊,AC為平行四邊形的對角線兩種切線討論即可解決問題.
試題解析:(1)拋物線的解析式為y=﹣![]() (x+4)(x﹣1),即
(x+4)(x﹣1),即![]() ;
;
(2)存在.
當x=0,y═![]() =2,則C(0,2),
=2,則C(0,2),
∴OC=2,
∵A(﹣4,0),B(1,0),
∴OA=4,OB=1,AB=5,
當∠PCB=90°時,
∵AC2=42+22=20,BC2=22+12=5,AB2=52=25
∴AC2+BC2=AB2
∴△ACB是直角三角形,∠ACB=90°,
∴當點P與點A重合時,△PBC是以BC為直角邊的直角三角形,此時P點坐標為(﹣4,0);
當∠PBC=90°時,PB∥AC,如圖1,
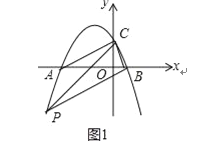
設直線AC的解析式為y=mx+n,
把A(﹣4,0),C(0,2)代入得![]() ,解得
,解得 ,
,
∴直線AC的解析式為y=![]() x+2,
x+2,
∵BP∥AC,
∴直線BP的解析式為y=![]() x+p,
x+p,
把B(1,0)代入得![]() +p=0,解得p=﹣
+p=0,解得p=﹣![]() ,
,
∴直線BP的解析式為y=![]() x﹣
x﹣![]() ,
,
解方程組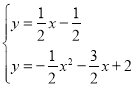 得
得![]() 或
或![]() ,此時P點坐標為(﹣5,﹣3);
,此時P點坐標為(﹣5,﹣3);
綜上所述,滿足條件的P點坐標為(﹣4,0),P2(﹣5,﹣3);
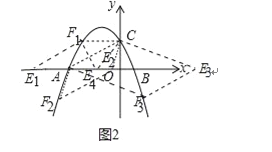
(3)存在點E,設點E坐標為(m,0),F(n,![]() )
)
①當AC為邊,CF1∥AE1,易知CF1=3,此時E1坐標(﹣7,0),
②當AC為邊時,AC∥EF,易知點F縱坐標為﹣2,
∴![]() =﹣2,解得n=
=﹣2,解得n=![]() ,得到F2(
,得到F2(![]() ,﹣2),F3(
,﹣2),F3(![]() ,﹣2),
,﹣2),
因此m=![]() 或
或![]() ,
,
此時E2(![]() ,0),E3(
,0),E3(![]() ,0),
,0),
③當AC為對角線時,AE4=CF1=3,此時E4(﹣1,0),
綜上所述滿足條件的點E為(﹣7,0)或(﹣1,0)或(![]() ,﹣2)或(
,﹣2)或(![]() ,﹣2).
,﹣2).


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】某校九年級(1)班全體學生體能測試成績統計如下表(總分30分):
成績(分) | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
人數(人) | 2 | 5 | 6 | 6 | 8 | 7 | 6 |
根據上表中的信息判斷,下列結論中錯誤的是( )
A. 該班一共有40名同學 B. 成績的眾數是28分
C. 成績的中位數是27分 D. 成績的平均數是27.45分
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com