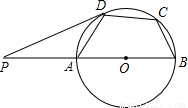
(2004•武漢)已知:二次函數y=ax2-(b-1)x-3a的圖象經過點P(4,10),交x軸于A(x1,0)、B(x2,0)兩點(x1<x2),交y軸負半軸于C點,且滿足3OA=OB.
(1)求二次函數的解析式;
(2)在二次函數的圖象上是否存在點M,使銳角∠MCO>∠ACO?若存在,請你求出M點的橫坐標的取值范圍;若不存在,請你說明理由.
【答案】
分析:(1)根據韋達定理和3OA=OB可得出一個關于a、b的等量關系式,將P點坐標代入拋物線中可得出另一個a、b的關系式,聯立兩個式子即可求出待定系數的值,也就得出了拋物線的解析式;
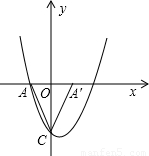
(2)如圖,取A點關于y軸的對稱點,那么∠A′CO=∠ACO,如果設直線A′C與拋物線的交點為N點話,那么如果使∠MCO>∠A′CO,那么必須滿足的條件為M的橫坐標在A的橫坐標與N的橫坐標之間,據此可求出M橫坐標的取值范圍(M的橫坐標不能為0,否則構不成銳角∠MCO).
解答:解:(1)∵P(4,10)在圖象上,
∴16a-4(b-1)-3a=10①;
∵圖象交y軸負半軸于C,
∴-3a<0,
∴a>0,x
1x
2=
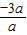
=-3<0,
∴x
1<0,x
2>0,x
2=-3x
1x
1+x
2=x
1+(-3x
1)=-2x
1=-
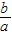
,x
1x
2=-3x
12=-3,
∴x
12=1,又x
1<0,
∴x
1=-1,
∴x
2=3,
∴b-1=2a②,
聯立①②解得:a=2,b=5,
∴y=2x
2-4x-6;
(2)存在點M,使∠MCO>∠ACO,A點關于y軸對稱點A′(1,0),
設直線A′C為y=kx+b,由于直線A′C過(1,0),(0,-6),則有:
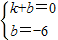
,
解得

.
∴y=6x-6,聯立拋物線的解析式有:
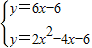
,
解得
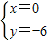
,

即直線A′C與拋物線交點為(0,-6),(5,24),
當y=-6時,即2x
2-4x-6=-6,
解得:x
1=0,x
2=2,
∵∠MCO是銳角,
∴符合題意的x的取值范圍是-1<x<0或2<x<5.
點評:本題主要考查了二次函數解析式的確定、韋達定理的應用、軸對稱圖形、函數圖象交點等知識.

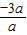 =-3<0,
=-3<0,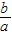 ,x1x2=-3x12=-3,
,x1x2=-3x12=-3,
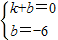 ,
, .
.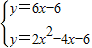 ,
,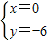 ,
,


 小題狂做系列答案
小題狂做系列答案