
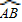 所在圓的圓心為O′時,求O′A的長度;
所在圓的圓心為O′時,求O′A的長度;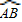 經過圓心為O時,求
經過圓心為O時,求 的長度;
的長度; 與
與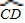 所在圓外切于點P時,設點O到弦AB、CD的距離之和為d,求d的值;
所在圓外切于點P時,設點O到弦AB、CD的距離之和為d,求d的值; 與
與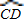 所在圓外切于點P時,設點M為AB的中點,點N為CD的中點,試探究四邊形OMPN的形狀,并證明你的結論.
所在圓外切于點P時,設點M為AB的中點,點N為CD的中點,試探究四邊形OMPN的形狀,并證明你的結論.
 所在圓O′與⊙O是等圓,可得O′A的長度;
所在圓O′與⊙O是等圓,可得O′A的長度; 的圓心角,再根據弧長公式計算即可;
的圓心角,再根據弧長公式計算即可; 所在圓的圓心O′到弦AB的距離;
所在圓的圓心O′到弦AB的距離; 與
與 所在圓外切于點P時,過點O作EF⊥AB交
所在圓外切于點P時,過點O作EF⊥AB交 于于點E,交
于于點E,交 于點F,根據折疊的性質,可求點O到AB、CD的距離之和;
于點F,根據折疊的性質,可求點O到AB、CD的距離之和; 解:(1)①折疊后的
解:(1)①折疊后的 所在圓O′與⊙O是等圓,
所在圓O′與⊙O是等圓, 經過圓O時,折疊后的
經過圓O時,折疊后的 所在圓O′在⊙O上,如圖2所示,連接O′A、OA、O′B,OB,OO′
所在圓O′在⊙O上,如圖2所示,連接O′A、OA、O′B,OB,OO′ =
= =
= ;
; ③如圖3所示,連接OA,OB,
③如圖3所示,連接OA,OB, .
. 與
與 所在圓外切于點P時,
所在圓外切于點P時, 于點E,交CD于點G、交
于點E,交CD于點G、交 于點F,
于點F, ∴EF垂直平分AB和CD,
∴EF垂直平分AB和CD, PE,PG=
PE,PG= PF,
PF, PE+
PE+ PF=
PF= (PE+PF)=2,
(PE+PF)=2, 所在圓的圓心為O′,折疊后的
所在圓的圓心為O′,折疊后的 所在圓的圓心為O″,
所在圓的圓心為O″, ∵點O′與點O關于AB對稱,點O″與點O關于CD對稱,
∵點O′與點O關于AB對稱,點O″與點O關于CD對稱, 與
與 所在圓外切,
所在圓外切, 與
與 所在圓與⊙O是等圓,
所在圓與⊙O是等圓, OO″=ON,
OO″=ON,

科目:初中數學 來源: 題型:
 |
| AB |
 |
| AB |
 |
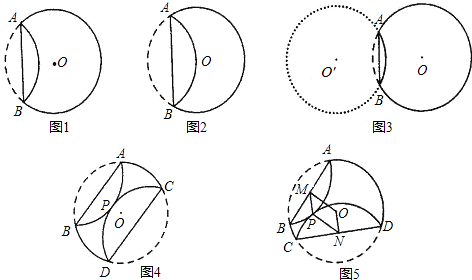
| AOB |
 |
| AB |
 |
| CD |
 |
| AB |
 |
| CD |

查看答案和解析>>
科目:初中數學 來源: 題型:
 |
| AB |
 |
| AB |
 |
| AB |
 |
| CD |
 |
| AB |
 |
| CD |
 |
| AB |
查看答案和解析>>
科目:初中數學 來源:2012年初中畢業(yè)升學考試(江西卷)數學(帶解析) 題型:解答題
已知,紙片⊙O的半徑為2,如圖1,沿弦AB折疊操作.
(1)①折疊后的 所在圓的圓心為O′時,求O′A的長度;
所在圓的圓心為O′時,求O′A的長度;
②如圖2,當折疊后的 經過圓心為O時,求
經過圓心為O時,求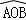 的長度;
的長度;
③如圖3,當弦AB=2時,求圓心O到弦AB的距離;
(2)在圖1中,再將紙片⊙O沿弦CD折疊操作.
①如圖4,當AB∥CD,折疊后的 與
與 所在圓外切于點P時,設點O到弦AB.CD的距離之和為d,求d的值;
所在圓外切于點P時,設點O到弦AB.CD的距離之和為d,求d的值;
②如圖5,當AB與CD不平行,折疊后的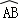 與
與 所在圓外切于點P時,設點M為AB的中點,點N為CD的中點,試探究四邊形OMPN的形狀,并證明你的結論.
所在圓外切于點P時,設點M為AB的中點,點N為CD的中點,試探究四邊形OMPN的形狀,并證明你的結論.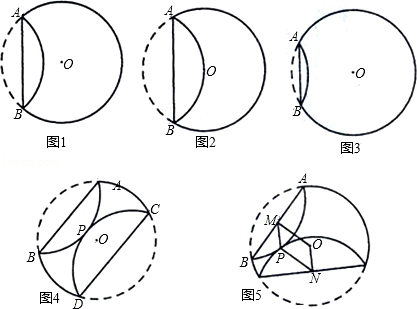
查看答案和解析>>
科目:初中數學 來源:2012年初中畢業(yè)升學考試(江西卷)數學(解析版) 題型:解答題
已知,紙片⊙O的半徑為2,如圖1,沿弦AB折疊操作.
(1)①折疊后的 所在圓的圓心為O′時,求O′A的長度;
所在圓的圓心為O′時,求O′A的長度;
②如圖2,當折疊后的 經過圓心為O時,求
經過圓心為O時,求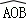 的長度;
的長度;
③如圖3,當弦AB=2時,求圓心O到弦AB的距離;
(2)在圖1中,再將紙片⊙O沿弦CD折疊操作.
①如圖4,當AB∥CD,折疊后的 與
與 所在圓外切于點P時,設點O到弦AB.CD的距離之和為d,求d的值;
所在圓外切于點P時,設點O到弦AB.CD的距離之和為d,求d的值;
②如圖5,當AB與CD不平行,折疊后的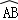 與
與 所在圓外切于點P時,設點M為AB的中點,點N為CD的中點,試探究四邊形OMPN的形狀,并證明你的結論.
所在圓外切于點P時,設點M為AB的中點,點N為CD的中點,試探究四邊形OMPN的形狀,并證明你的結論.
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com