
【題目】已知:如圖所示,在![]() 中,過
中,過![]() ,
,![]() 作
作![]() 的垂線垂足為
的垂線垂足為![]() ,
,![]() ,過
,過![]() ,
,![]() 作
作![]() 的垂線,垂足為
的垂線,垂足為![]() ,
,![]() (
(![]() ,
,![]() 不垂直).
不垂直).
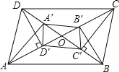
(1)試說明:四邊形![]() ;
;
(2)四邊形![]() 與
與![]() 是不是位似圖形.
是不是位似圖形.
【答案】(1)證明見解析;(2)四邊形![]() 與
與![]() 不是位似圖形;
不是位似圖形;
【解析】
(1)根據(jù)垂直的定義得到∠AA’D=∠AD’D=90°,得到A、D’、A’、D四點共圓,證明OAD∽△OA’D’,根據(jù)相似三角形的性質(zhì)證明![]() ,∠ADC=∠A’D’C’,繼而則可證明結(jié)論;
,∠ADC=∠A’D’C’,繼而則可證明結(jié)論;
(2)根據(jù)位似圖形的對應(yīng)邊互相平行進(jìn)行判斷即可.
(1)∵![]() ’
’![]() ’
’![]() ,
,
∴![]() 、
、![]() ’、
’、![]() ’、
’、![]() 四點共圓,
四點共圓,
∴![]() ’
’![]() ’
’![]() ’,
’,
∵![]() ’,
’,![]() ’
’![]() ’
’![]() ’
’![]() (直角三角形的銳角互補),
(直角三角形的銳角互補),
∴![]() ’
’![]() ’,
’,
∴![]() ’
’![]() ’,
’,
∴![]() ,
,![]() ’
’![]() ,
,
同理可證:![]() ,
,![]() ’
’![]() ’,
’,
∵![]() ’
’![]() ’
’![]() ’
’![]() ’,
’,![]() ’
’![]() ’,
’,
∴![]() ,
,
∴![]() ,
,
同理可證:![]() ’
’![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ’
’![]() ,
,
∴![]() ’
’![]() ’
’![]() ’
’![]() ’
’![]() ’,
’,
∴平行四邊形![]() 平行四邊形
平行四邊形![]() ’
’![]() ’
’![]() ’
’![]() ’相似;
’相似;
(2)∵![]() 與
與![]() 不平行,
不平行,
∴四邊形![]() 與
與![]() 不是位似圖形.
不是位似圖形.


 名校課堂系列答案
名校課堂系列答案科目:初中數(shù)學(xué) 來源: 題型:
【題目】開口向下的拋物線y=a(x+1)(x-9)與x軸交于A、B兩點,與y軸交于點C,若∠ACB=90°,則a的值為________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() 和
和![]() 的平分線相交于點
的平分線相交于點![]() ,過點
,過點![]() 作
作![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,過點
,過點![]() 作
作![]() 于
于![]() 下列結(jié)論:①
下列結(jié)論:①![]() ;②點
;②點![]() 到
到![]() 各邊的距離相等;③
各邊的距離相等;③![]() ;④設(shè)
;④設(shè)![]() ,
,![]() ,則
,則![]() ;⑤
;⑤![]() .其中正確的結(jié)論是.__________.
.其中正確的結(jié)論是.__________.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某商場一種商品的進(jìn)價為每件30元,售價為每件40元.每天可以銷售48件,為盡快減少庫存,商場決定降價促銷.
(1)若該商品連續(xù)兩次下調(diào)相同的百分率后售價降至每件32.4元,求兩次下降的百分率;
(2)經(jīng)調(diào)查,若每降價0.5元,每天可多銷售4件,那么每天要想獲得510元的利潤,每件應(yīng)降價多少元?

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知矩形 OABC,以點 O 為坐標(biāo)原點建立平面直角坐標(biāo)系,其中 A(2,0), C(0,3),點 P 以每秒 1 個單位的速度從點 C 出發(fā)在射線 CO 上運動,連接 BP,作 BE⊥PB 交 x 軸于點 E,連接 PE 交 AB 于點 F,設(shè)運動時間為 t 秒.
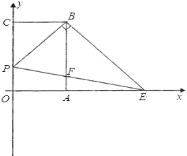
(1)當(dāng) t=2 時,求點 E 的坐標(biāo);
(2)在運動的過程中,是否存在以 P、O、E 為頂點的三角形與△PCB 相似.若存在,請求出點 P 的坐標(biāo);若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在![]() 中,如果一條直角邊和斜邊的長度都縮小至原來的
中,如果一條直角邊和斜邊的長度都縮小至原來的![]() ,那么銳角
,那么銳角![]() 的各個三角函數(shù)值( )
的各個三角函數(shù)值( )
A. 都縮小![]() B. 都不變 C. 都擴(kuò)大
B. 都不變 C. 都擴(kuò)大![]() 倍 D. 無法確定
倍 D. 無法確定
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的兩條角平分線,且
的兩條角平分線,且![]() ,
,![]() 交于點
交于點![]() .
.
(1)如圖1,用等式表示![]() ,
,![]() ,
,![]() 這三條線段之間的數(shù)量關(guān)系,并證明你的結(jié)論;
這三條線段之間的數(shù)量關(guān)系,并證明你的結(jié)論;

小東通過觀察、實驗,提出猜想:![]() .他發(fā)現(xiàn)先在
.他發(fā)現(xiàn)先在![]() 上截取
上截取![]() ,使
,使![]() ,連接
,連接![]() ,再利用三角形全等的判定和性質(zhì)證明
,再利用三角形全等的判定和性質(zhì)證明![]() 即可.
即可.
①下面是小東證明該猜想的部分思路,請補充完整:
ⅰ)在![]() 上截取
上截取![]() ,使
,使![]() ,連接
,連接![]() ,則可以證明
,則可以證明![]() 與 全等,判定它們?nèi)鹊囊罁?jù)是 ;
與 全等,判定它們?nèi)鹊囊罁?jù)是 ;
ⅱ)由![]() ,
,![]() ,
,![]() 是
是![]() 的兩條角平分線,可以得出
的兩條角平分線,可以得出![]() °;
°;
②請直接利用ⅰ),ⅱ)已得到的結(jié)論,完成證明猜想![]() 的過程.
的過程.
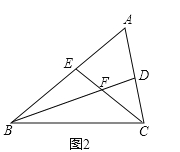
(2)如圖2,若![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在直徑為1000毫米的圓柱形油罐內(nèi)裝進(jìn)一些油.其橫截面如圖.油面寬AB=600毫米.
(1)求油的最大深度;
(2)如果再注入一些油后,油面寬變?yōu)?/span>800毫米,此時油面上升了多少毫米?

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】二次函數(shù)y=ax2+bx+c(a≠0)的圖象經(jīng)過點A(3,0),B(2,﹣3),并且以x=1為對稱軸.
(1)求此函數(shù)的解析式;
(2)作出二次函數(shù)的大致圖象;
(3)在對稱軸x=1上是否存在一點P,使△PAB中PA=PB?若存在,求出P點的坐標(biāo);若不存在,說明理由.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com