
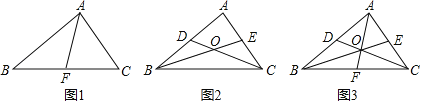
【題目】問題解決:如圖1,△ABC中,AF為BC邊上的中線,則S△ABF= S△ABC.
問題探究:
(1)如圖2,CD,BE分別是△ABC的中線,S△BOC與S四邊形ADOE相等嗎?
解:△ABC中,由問題解決的結論可得,S△BCD=![]() S△ABC,S△ABE=
S△ABC,S△ABE=![]() S△ABC.
S△ABC.
∴S△BCD=S△ABE
∴S△BCD﹣S△BOD=S△ABE﹣S△BOD
即S△BOC=S四邊形ADOE.
(2)圖2中,仿照(1)的方法,試說明S△BOD=S△COE.
(3)如圖3,CD,BE,AF分別是△ABC的中線,則S△BOC= S△ABC,S△AOE= S△ABC,S△BOD= S△ABF.
問題拓展:
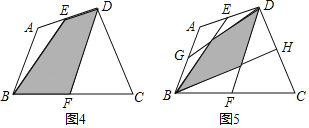
(4)①如圖4,E、F分別為四邊形ABCD的邊AD、BC的中點,請直接寫出陰影部分的面積與四邊形ABCD的面積之間的數量關系:S陰影= S四邊形ABCD.
②如圖5,E、F、G、H分別為四邊形ABCD的邊AD、BC、AB、CD的中點,請直接寫出陰影部分的面積與四邊形ABCD的面積之間的數量關系:S陰影= S四邊形ABCD.
【答案】問題解決:![]() ;問題探究:(2)證明見解析;(3)
;問題探究:(2)證明見解析;(3)![]() ,
,![]() ,
,![]() ;問題拓展:(4)①
;問題拓展:(4)①![]() ;②
;②![]() .
.
【解析】
問題解決:根據中線的性質即可得出結論;
問題探究:(2)根據問題解決的結論可得,S△BCD=![]() S△ABC,S△BCE=
S△ABC,S△BCE=![]() S△ABC,然后根據等式的基本性質即可得出S△BOD=S△COE;
S△ABC,然后根據等式的基本性質即可得出S△BOD=S△COE;
(3)根據中線的性質和探究結論(1)(2)可推出S△AOE=S△AOD=S△BOF=S△COF=S△BOD=S△COE=![]() S△ABC,從而得出結論;
S△ABC,從而得出結論;
問題拓展:(4)①連接BD,根據中線的性質可得S△ABE=S△BDE和S△BDF=S△DFC,從而得出結論;②連接BD,設BE交DG于M,BH交DF于N,根據問題探究:(3)的結論,可得S△BDM=![]() S△ABD,S△BDN=
S△ABD,S△BDN=![]() S△BDC,,從而得出結論.
S△BDC,,從而得出結論.
解:問題解決:∵AF是BC邊上的中線,
∴S△ABF=S△AFC,
∴S△ABF=![]() S△ABC,
S△ABC,
故答案為![]() .
.
問題探究:(2)△ABC中,由問題解決的結論可得,S△BCD=![]() S△ABC,S△BCE=
S△ABC,S△BCE=![]() S△ABC.
S△ABC.
∴S△BCD=S△BCE
∴S△BCD﹣S△BOC=S△BCE﹣S△BOC
∴S△BOD=S△COE.
(3)∵CD,BE,AF分別是△ABC的中線,
∴S△BOF=S△COF, S△BAF=S△CAF,S△BOD=S△AOD,
利用探究結論(1)(2)易證:S△BOC=S四邊形ADOE, S△BOD=S△COE
∴S△AOD=S△BAF-S△BOD-S△BOF=S△CAF-S△COE-S△COF=S△AOE
∴S△BOC=2S△BOF,S四邊形ADOE=2S△AOD
∴S△BOF=S△AOD
∴S△AOE=S△AOD=S△BOF=S△COF=S△BOD=S△COE=![]() S△ABC,
S△ABC,
S△BOC=2S△BOF=![]() S△ABC,S△AOE=
S△ABC,S△AOE=![]() S△ABC,S△BOD=
S△ABC,S△BOD=![]() S△ABF.
S△ABF.
故答案為![]() ,
,![]() ,
,![]() .
.
問題拓展:(4)①如圖4中,連接BD.

∵BE是△ABD的中線,
∴S△ABE=S△BDE,
∵DF是△BCD的中線,
∴S△BDF=S△DFC,
∴S陰=![]() S四邊形ABCD,
S四邊形ABCD,
故答案為![]() .
.
②如圖5中,連接BD,設BE交DG于M,BH交DF于N.
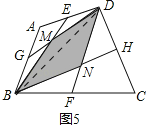
用問題探究可知:S△BDM=![]() S△ABD,S△BDN=
S△ABD,S△BDN=![]() S△BDC,
S△BDC,
∴S陰=![]() (S△ABD+S△BDC)=
(S△ABD+S△BDC)=![]() S四邊形ABCD,
S四邊形ABCD,
故答案為![]() .
.


 提分百分百檢測卷系列答案
提分百分百檢測卷系列答案 寶貝計劃期末沖刺奪100分系列答案
寶貝計劃期末沖刺奪100分系列答案科目:初中數學 來源: 題型:
【題目】計算下列各題:
(1) 4+(1)=___ ;(2) 3(2)=___;(3)2×4=___;(4)6÷(2)=___;(5)5+(1)2=___;(6)1÷3×![]() =___.
=___.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:在△ABC中,BE、CF分別是AC、AB兩邊上的高,在BE上截取BD=AC,在CF的延長線上截取CG=AB,連接AD、AG.
(1)求證:AD=AG;
(2)AD與AG的位置關系如何,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有20筐白菜,以每筐30千克為標準,超過或不足的分別用正、負來表示,記錄如下:
與標準質量的差(單位:千克) | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
筐數 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)20筐白菜中,最重的一筐比最輕的一筐要重多少千克?
(2)與標準質量比較,20筐白菜總計超過或不足多少千克?
(3)若白菜每千克售價2元,則出售這20筐白菜可賣多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1、2,已知四邊形ABCD為正方形,在射線AC上有一動點P,作PE⊥AD(或延長線)于E,作PF⊥DC(或延長線)于F,作射線BP交EF于G.
(1)在圖1中,設正方形ABCD的邊長為2,四邊形ABFE的面積為y,AP=x,求y關于x的函數表達式;
(2)結論:GB⊥EF對圖1,圖2都是成立的,請任選一圖形給出證明;
(3)請根據圖2證明:△FGC∽△PFB.

查看答案和解析>>
科目:初中數學 來源: 題型:
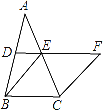
【題目】如圖,在△ABC中,D、E分別是AB、AC的中點,BE=2DE,延長DE到點F,使得EF=BE,連接CF.
(1)求證:四邊形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,一方隊正沿箭頭所指的方向前進

(1)A的位置為第三列第四行,表示為(3,4),那么B的位置是____________.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(2)B左側第二個人的位置是____________.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(3)如果隊伍向東前進,那么A北側第二個人的位置是____________.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(4)![]() 表示的位置是____________.
表示的位置是____________.
A.A B.B C.C D.D
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,邊AB的長為3,點E,F分別在AD,BC上,連接BE,DF,EF,BD.若四邊形BEDF是菱形,且EF=AE+FC,則邊BC的長為( )

A. 2![]() B. 3
B. 3![]() C. 6
C. 6![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90,AC=BC,AD平分∠CAB,DE⊥AB,垂足為E.
(1)求證:CD=BE;
(2)若AB=10,求BD的長度。

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com