
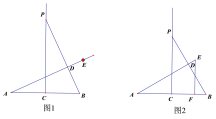
【題目】(1)操作發現:如圖1,D是等邊三角形ABC邊BA上一動點(點D與點B不重合),連接DC,以DC為邊在BC上方作等邊三角形DCF,連接AF.你能發現線段AF與BD之間的數量關系嗎?并證明你發現的結論.
(2)類比猜想:如圖2,當動點D運動到等邊三角形ABC邊BA的延長線上時,其他作法與(1)相同,猜想AF與BD在(1)中的結論是否仍然成立?如果成立,請證明;如果不成立,是否有新的結論?如果有新的結論,直接寫出新的結論,不需證明.
(3)深入探究:①如圖3,當動點D在等邊三角形ABC的邊BA上運動時(點D與點B不重合),連接DC,以DC為邊在其上方、下方分別作等邊三角形DCF和等邊三角形DCF',連接AF,BF′.探究AF,BF′與AB有何數量關系?并證明你發現的結論。
②如圖4,當動點D在等邊三角形ABC的邊BA的延長線上運動時,其他作法與圖3相同,①中的結論是否仍然成立?如果成立,請證明;如果不成立,是否有新的結論?如果有新的結論,直接寫出新的結論,不需證明.

【答案】(1)BD=AF,理由見解析;(2)成立,BD=AF,理由見解析;(3)①AB=AF+BF',理由見解析;②不成立,新結論為AB=AF-BF',理由見解析
【解析】
(1)證明△BCD≌△ACF即可解題;
(2)證明△BCD≌△ACF即可解題;
(3)①證明△BCD≌△ACF和△BCF'≌△ACD可得BD=AF和AD=BF'即可解題;
②證明△BCD≌△ACF和△BCF'≌△ACD可得BD=AF和AD=BF'即可證明新結論.
(1)∵∠BCA=∠DCF,
∴∠BCD=∠ACF,
在△BCD和△ACF中,
BC=AC,∠BCD=∠ACF,CF=CD,
∴△BCD≌△ACF,(SAS),
∴BD=AF;
(2)∵∠BCA=∠DCF,
∴∠BCD=∠ACF,
在△BCD和△ACF中,
BC=AC,∠BCD=∠ACF,CF=CD,
∴△BCD≌△ACF(SAS),
∴BD=AF;
(3)①∵∠BCA=∠DCF,
∴∠BCD=∠ACF,
在△BCD和△ACF中,
BC=AC,∠BCD=∠ACF,CF=CD,
∴△BCD≌△ACF(SAS),
∴BD=AF
∵∠BCA=∠DCF',
∴∠BCF'=∠ACD,
在△BCF'和△ACD中,
BC=AC,∠ACD=∠BCF,′CD=CF′,
∴△BCF'≌△ACD(SAS),
∴AD=BF',
∴AB=AF+BF';
②不成立,新結論為AB=AF-BF'.
證明∵∠BCA=∠DCF,
∴∠BCD=∠ACF,
在△BCD和△ACF中,
BC=AC,∠BCD=∠ACF,CF=CD,
∴△BCD≌△ACF(SAS),
∴BD=AF;
∵∠BCA=∠DCF',
∴∠BCF'=∠ACD,
在△BCF'和△ACD中,
BC=AC,∠ACD=∠BCF′,CD=CF′,
∴△BCF'≌△ACD(SAS),
∴AD=BF',
∴AB=AF-BF'.


科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD中,AE平分∠BAD,DE平分∠ADC.

(1)如果∠B+∠C=120°,則∠AED的度數=______.(直接寫出結果)
(2)根據⑴的結論,猜想∠B+∠C與∠AED之間的關系,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線AB、CD相交于點O,OE把∠BOD分成兩部分;
(1)直接寫出圖中∠AOC的對頂角為 ,∠BOE的鄰補角為 ;
(2)若∠AOC=70°,且∠BOE:∠EOD=2:3,求∠AOE的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,已知點![]() 是線段
是線段![]() 的中點,過點
的中點,過點![]() 作
作![]() 的垂線
的垂線![]() ,在射線
,在射線![]() 上有一個動點
上有一個動點![]() (點
(點![]() 不與端點
不與端點![]() 重合),連接
重合),連接![]() ,過點
,過點![]() 作
作![]() 的垂線,垂足為點
的垂線,垂足為點![]() ,在射線
,在射線![]() 上取點
上取點![]() ,使得
,使得![]() ,已知
,已知![]()
(1)當![]() 時,求
時,求![]() 的度數;
的度數;
(2)過點![]() 作
作![]() 垂直于直線
垂直于直線![]() 交
交![]() 于點
于點![]() ,在點
,在點![]() 的運動過程中,
的運動過程中,![]() 的大小隨點
的大小隨點![]() 的運動而變化,在這個變化過程中線段
的運動而變化,在這個變化過程中線段![]() 的長度是否發生變化?若不變,求出
的長度是否發生變化?若不變,求出![]() 的長;若變化,請說明理由;
的長;若變化,請說明理由;
(3)如圖2,當![]() 時,設直線
時,設直線![]() 與直線
與直線![]() 相交于點
相交于點![]() ,求
,求![]() 的度數.
的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,下列能判定AB∥CD的條件有( )個.
(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在四邊形![]() 中,
中,![]() 是
是![]() 邊上一點,
邊上一點,![]() 點
點![]() 從
從![]() 出發以
出發以![]() 秒的速度沿線段
秒的速度沿線段![]() 運動,同時點
運動,同時點![]() 從
從![]() 出發,沿線段
出發,沿線段![]() 、射線
、射線![]() 運動,當
運動,當![]() 運動到
運動到![]() ,兩點都停止運動.設運動時間為
,兩點都停止運動.設運動時間為![]() (秒):
(秒):

(1)當![]() 與
與![]() 的速度相同,且
的速度相同,且![]() 時,求證:
時,求證:![]()
(2)當![]() 與
與![]() 的速度不同,且
的速度不同,且![]() 分別在
分別在![]() 上運動時(如圖1),若
上運動時(如圖1),若![]() 與
與![]() 全等,求此時
全等,求此時![]() 的速度和
的速度和![]() 值;
值;
(3)當![]() 運動到
運動到![]() 上,
上,![]() 運動到射線
運動到射線![]() 上(如圖2),若
上(如圖2),若![]() 的速度為
的速度為![]() 秒,是否存在恰當的邊
秒,是否存在恰當的邊![]() 的長,使在運動過程中某一時刻剛好
的長,使在運動過程中某一時刻剛好![]() 與
與![]() 全等,若存在,請求出此時
全等,若存在,請求出此時![]() 的值和邊
的值和邊![]() 的長;若不存在,請說明理由.
的長;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ABC與∠ACB的平分線交于點O,過點O作DE∥BC,分別交AB、AC于點D、E.

(1)△BDO是等腰三角形嗎?請說明理由.
(2)若AB=10,AC=6,求△ADE的周長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com