
【題目】定義:如圖①,拋物線y=ax2+bx+c(a≠0)與x軸交于A,B兩點,點P在該拋物線上(P點與A、B兩點不重合).如果△ABP的三邊滿足AP2+BP2=AB2,則稱點P為拋物線y=ax2+bx+c(a≠0)的勾股點.
(1)直接寫出拋物線y=-x2+1的勾股點的坐標.
(2)如圖②,已知拋物線y=ax2+bx(a≠0)與x軸交于A,B兩點,點P(1, ![]() )是拋物線的勾股點,求拋物線的函數表達式.
)是拋物線的勾股點,求拋物線的函數表達式.
(3)在(2)的條件下,點Q在拋物線上,求滿足條件S△ABQ=S△ABP的Q點(異于點P)的坐標.

【答案】(1)(0,1)(2) y=-![]() x(x-4)=-
x(x-4)=-![]() x2+
x2+![]() x(3)滿足條件的點Q有3個,分別為(3,
x(3)滿足條件的點Q有3個,分別為(3, ![]() )或(2+
)或(2+![]() ,-
,- ![]() )或(2-
)或(2-![]() ,-
,- ![]() ).
).
【解析】試題分析:(1)根據拋物線勾股點的定義可以求解,(2)作PG⊥x軸,由點P的坐標求得:AG=1,PG=![]() ,由三角函數可得:
,由三角函數可得: ![]() ,可知∠PAG=60°從而求得AB=4,即B(4,0),待定系數法可求解得,(3)由
,可知∠PAG=60°從而求得AB=4,即B(4,0),待定系數法可求解得,(3)由![]() 且兩個三角形同底,可知點Q到x軸的距離為
且兩個三角形同底,可知點Q到x軸的距離為![]() ,即可求解.
,即可求解.
(1)拋物線y=-x2+1的勾股點的坐標為(0,1).
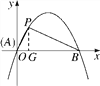
(2)如圖,作PG⊥x軸于點G.∵點P的坐標為(1,![]() ),∴AG=1,PG=
),∴AG=1,PG=![]() ,∴PA=
,∴PA=![]() =
=![]() =2.∵tan∠PAB=
=2.∵tan∠PAB=![]() =
=![]() ,∴∠PAG=60°.在Rt△PAB中,AB=
,∴∠PAG=60°.在Rt△PAB中,AB=![]() =
=![]() =4,∴點B的坐標為(4,0).
=4,∴點B的坐標為(4,0).
設y=ax(x-4),將點P(1,![]() )代入得a=-
)代入得a=-![]() ,∴y=-
,∴y=-![]() x(x-4)=-
x(x-4)=-![]() x2+
x2+![]() x.
x.
(3)①當點Q在x軸上方時,由S△ABQ=S△ABP知點Q的縱坐標為![]() ,則有-
,則有-![]() x2+
x2+![]() x=
x=![]() ,解得x1=3,x2=1(不符合題意,舍去),∴點Q的坐標為(3,
,解得x1=3,x2=1(不符合題意,舍去),∴點Q的坐標為(3,![]() ).
).
②當點Q在x軸下方時,由S△ABQ=S△ABP知點Q的縱坐標為-![]() ,則有-
,則有-![]() x2+
x2+![]() x=-
x=-![]() ,解得x1=2+
,解得x1=2+![]() ,x2=2-
,x2=2-![]() ,∴點Q的坐標為(2+
,∴點Q的坐標為(2+![]() ,-
,-![]() )或(2-
)或(2-![]() ,-
,-![]() ).
).
綜上所述,滿足條件的點Q有3個,分別為(3,![]() )或(2+
)或(2+![]() ,-
,-![]() )或(2-
)或(2-![]() ,-
,-![]() ).
).


科目:初中數學 來源: 題型:
【題目】已知數軸上點A表示的數為6,B是數軸上在左側的一點,且A,B兩點間的距離為10。動點P從點A出發,以每秒6個單位長度的度沿數軸向左勻速運動,設運動時間為t![]() 秒。
秒。
![]()
(1)數軸上點B表示的數是______;當點P運動到AB的中點時,它所表示的數是_____。
(2)動點Q從點B出發,以每秒2個單位長度的速度沿數軸向左勻速運動,若點P、Q同時出發,求:
①當點P運動多少秒時,點P追上點Q?
②當點P運動多少秒時,點P與點Q間的距離為8個單位長度?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,下列圖案均是長度相同的火柴按一定的規律拼搭而成:第1個圖案需7根火柴,第2個圖案需13根火柴,…,依此規律,第11個圖案需( )根火柴.

A. 156 B. 157 C. 158 D. 159
查看答案和解析>>
科目:初中數學 來源: 題型:
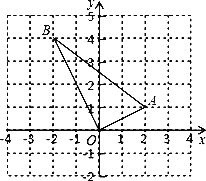
【題目】已知:如圖,△OAB,點O為原點,點A、B的坐標分別是(2,1)、(﹣2,4).
(1)若點A、B都在一次函數y=kx+b圖象上,求k,b的值;
(2)求△OAB的邊AB上的中線的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,為美化環境,某校計劃在一塊長為60米,寬為40米的長方形空地上修建一個長方形花圃,并將花圃四周余下的空地修建成同樣寬的通道,設通道寬為a米.
(1)用含a的式子表示花圃的面積;
(2)如果通道所占面積是整個長方形空地面積的![]() ,求出此時通道的寬.
,求出此時通道的寬.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=8,AD=6,點E為AB上一點,AE=2![]() ,點F在AD上,將△AEF沿EF折疊,當折疊后點A的對應點A'恰好落在BC的垂直平分線上時,折痕EF的長為__________
,點F在AD上,將△AEF沿EF折疊,當折疊后點A的對應點A'恰好落在BC的垂直平分線上時,折痕EF的長為__________

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】李明準備進行如下操作實驗,把一根長40 cm的鐵絲剪成兩段,并把每段首尾相連各圍成一個正方形.
(1)要使這兩個正方形的面積之和等于58 cm2,李明應該怎么剪這根鐵絲?
(2)李明認為這兩個正方形的面積之和不可能等于48 cm2,你認為他的說法正確嗎?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】乒乓球是我國的國球,也是世界上流行的球類體育項目.我國乒乓球名將與其對應身高如下表所示:
乒乓球名將 | 劉詩雯 | 鄧亞萍 | 白楊 | 丁寧 | 陳夢 | 孫穎莎 | 姚彥 |
身高( | 160 | 155 | 171 | 173 | 163 | 160 | 175 |
這些乒乓球名將身高的中位數和眾數是( )
A.160,163B.173,175C.163,160D.172,160
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知二次函數y=ax2+bx+4的圖象與x軸交于點B(-2,0),點C(8,0),與y軸交于點A.
(1)求二次函數y=ax2+bx+4的表達式;
(2)連接AC,AB,若點N在線段BC上運動(不與點B,C重合),過點N作NM∥AC,交AB于點M,當△AMN面積最大時,求N點的坐標;
(3)連接OM,在(2)的結論下,求OM與AC的數量關系.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com