
【題目】如圖,在平面直角坐標(biāo)系中,拋物線y=ax2+2x+c與x軸交于A(﹣1,0)B(3,0)兩點(diǎn),與y軸交于點(diǎn)C,點(diǎn)D是該拋物線的頂點(diǎn).
(1)求拋物線的解析式和直線AC的解析式;
(2)請?jiān)?/span>y軸上找一點(diǎn)M,使△BDM的周長最小,求出點(diǎn)M的坐標(biāo);
(3)試探究:在拋物線上是否存在點(diǎn)P,使以點(diǎn)A,P,C為頂點(diǎn),AC為直角邊的三角形是直角三角形?若存在,請求出符合條件的點(diǎn)P的坐標(biāo);若不存在,請說明理由.
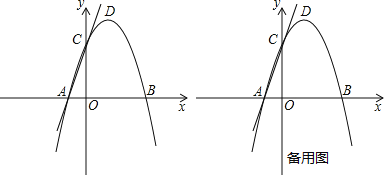
【答案】(1)拋物線解析式為y=﹣x2+2x+3;直線AC的解析式為y=3x+3;(2)點(diǎn)M的坐標(biāo)為(0,3);
(3)符合條件的點(diǎn)P的坐標(biāo)為(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() ),
),
【解析】(1)設(shè)交點(diǎn)式y=a(x+1)(x-3),展開得到-2a=2,然后求出a即可得到拋物線解析式;再確定C(0,3),然后利用待定系數(shù)法求直線AC的解析式;
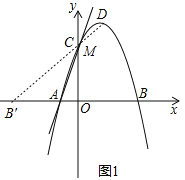
(2)利用二次函數(shù)的性質(zhì)確定D的坐標(biāo)為(1,4),作B點(diǎn)關(guān)于y軸的對稱點(diǎn)B′,連接DB′交y軸于M,如圖1,則B′(-3,0),利用兩點(diǎn)之間線段最短可判斷此時(shí)MB+MD的值最小,則此時(shí)△BDM的周長最小,然后求出直線DB′的解析式即可得到點(diǎn)M的坐標(biāo);
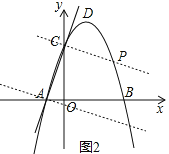
(3)過點(diǎn)C作AC的垂線交拋物線于另一點(diǎn)P,如圖2,利用兩直線垂直一次項(xiàng)系數(shù)互為負(fù)倒數(shù)設(shè)直線PC的解析式為y=-![]() x+b,把C點(diǎn)坐標(biāo)代入求出b得到直線PC的解析式為y=-
x+b,把C點(diǎn)坐標(biāo)代入求出b得到直線PC的解析式為y=-![]() x+3,再解方程組
x+3,再解方程組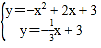 得此時(shí)P點(diǎn)坐標(biāo);當(dāng)過點(diǎn)A作AC的垂線交拋物線于另一點(diǎn)P時(shí),利用同樣的方法可求出此時(shí)P點(diǎn)坐標(biāo).
得此時(shí)P點(diǎn)坐標(biāo);當(dāng)過點(diǎn)A作AC的垂線交拋物線于另一點(diǎn)P時(shí),利用同樣的方法可求出此時(shí)P點(diǎn)坐標(biāo).
(1)設(shè)拋物線解析式為y=a(x+1)(x﹣3),
即y=ax2﹣2ax﹣3a,
∴﹣2a=2,解得a=﹣1,
∴拋物線解析式為y=﹣x2+2x+3;
當(dāng)x=0時(shí),y=﹣x2+2x+3=3,則C(0,3),
設(shè)直線AC的解析式為y=px+q,
把A(﹣1,0),C(0,3)代入得![]() ,解得
,解得![]() ,
,
∴直線AC的解析式為y=3x+3;
(2)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴頂點(diǎn)D的坐標(biāo)為(1,4),
作B點(diǎn)關(guān)于y軸的對稱點(diǎn)B′,連接DB′交y軸于M,如圖1,則B′(﹣3,0),
∵MB=MB′,
∴MB+MD=MB′+MD=DB′,此時(shí)MB+MD的值最小,
而BD的值不變,
∴此時(shí)△BDM的周長最小,
易得直線DB′的解析式為y=x+3,
當(dāng)x=0時(shí),y=x+3=3,
∴點(diǎn)M的坐標(biāo)為(0,3);
(3)存在.
過點(diǎn)C作AC的垂線交拋物線于另一點(diǎn)P,如圖2,
∵直線AC的解析式為y=3x+3,
∴直線PC的解析式可設(shè)為y=﹣![]() x+b,
x+b,
把C(0,3)代入得b=3,
∴直線PC的解析式為y=﹣![]() x+3,
x+3,
解方程組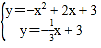 ,解得
,解得![]() 或
或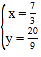 ,則此時(shí)P點(diǎn)坐標(biāo)為(
,則此時(shí)P點(diǎn)坐標(biāo)為(![]() ,
,![]() );
);
過點(diǎn)A作AC的垂線交拋物線于另一點(diǎn)P,直線PC的解析式可設(shè)為y=﹣![]() x+b,
x+b,
把A(﹣1,0)代入得![]() +b=0,解得b=﹣
+b=0,解得b=﹣![]() ,
,
∴直線PC的解析式為y=﹣![]() x﹣
x﹣![]() ,
,
解方程組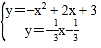 ,解得
,解得![]() 或
或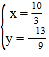 ,則此時(shí)P點(diǎn)坐標(biāo)為(
,則此時(shí)P點(diǎn)坐標(biāo)為(![]() ,﹣
,﹣![]() ).
).
綜上所述,符合條件的點(diǎn)P的坐標(biāo)為(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() ).
).



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
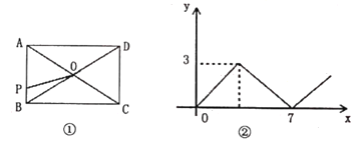
【題目】如圖①,在矩形ABCD中,AB<AD,對角線AC,BD相交于點(diǎn)O,動點(diǎn)P由點(diǎn)A出發(fā),沿AB-BC→CD向點(diǎn)D運(yùn)動設(shè)點(diǎn)P的運(yùn)動路程為x,△AOP的面積為y,y與x的函數(shù)關(guān)系圖象如圖②所小示,則AD的長為________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
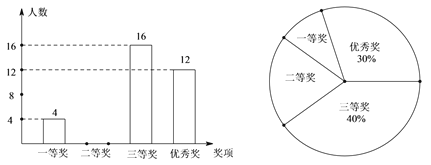
【題目】某中學(xué)在全校學(xué)生中開展了“地球—我們的家園”為主題的環(huán)保征文比賽,評選出一、二、三等獎和優(yōu)秀獎。根據(jù)獎項(xiàng)的情況繪制成如圖所示的兩幅不完整的統(tǒng)計(jì)圖,請你根據(jù)圖中提供的信息解答下列問題:
(1)求校獲獎的總?cè)藬?shù),并把條形統(tǒng)計(jì)圖補(bǔ)充完整;
(2)求在扇形統(tǒng)計(jì)圖中表示“二等獎” 的扇形的圓心角的度數(shù);
(3)獲得一等獎的4名學(xué)生中有3男1女,現(xiàn)打算從中隨機(jī)選出2名學(xué)生參加頒獎活動,請用列表或畫樹狀圖的方法求選出的2名學(xué)生恰好是1男1女的概率﹒
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知等邊△ABC的邊長為8,以AB為直徑的圓交BC于點(diǎn)F.以C為圓心,CF長為半徑作圖,D是⊙C上一動點(diǎn),E為BD的中點(diǎn),當(dāng)AE最大時(shí),BD的長為( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 12
D. 12
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,拋物線y = x2+bx+c過點(diǎn)A (-1,2),且關(guān)于y軸對稱,點(diǎn)C與點(diǎn)B(a,0)(a>1)關(guān)于原點(diǎn)對稱,直線AC交拋物線于點(diǎn)D.
(1)求此拋物線的解析式;
(2)連接OA,BD,當(dāng)OA//BD時(shí),求a的值;
(3)若直線AC交拋物線![]() 于E,F兩點(diǎn)(點(diǎn)E在點(diǎn)F的左側(cè)),且EA=DF,求直線AC的解析式.
于E,F兩點(diǎn)(點(diǎn)E在點(diǎn)F的左側(cè)),且EA=DF,求直線AC的解析式.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知關(guān)于x的方程![]()
(1)求證:不論k取什么實(shí)數(shù)值,這個(gè)方程總有實(shí)數(shù)根;
(2)若等腰三角形ABC的一邊長為![]() ,另兩邊的長b、c恰好是這個(gè)方程的兩個(gè)根,求△ABC的周長.
,另兩邊的長b、c恰好是這個(gè)方程的兩個(gè)根,求△ABC的周長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某體育文化用品商店購進(jìn)籃球和排球共200個(gè),進(jìn)價(jià)和售價(jià)如下表全部銷售完后共獲利潤2600元.
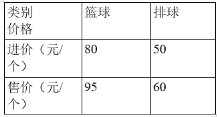
(1)求商店購進(jìn)籃球和排球各多少個(gè)?
(2)王老師在元旦節(jié)這天到該體育文化用品商店為學(xué)校買籃球和排球各若干個(gè)(兩種球都買了),商店在他的這筆交易中獲利100元王老師有哪幾種購買方案.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
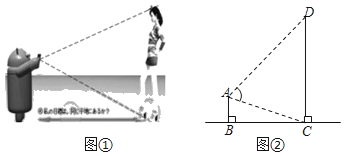
【題目】智能手機(jī)如果安裝了一款測量軟件“SmartMeasure”后,就可以測量物高、寬度和面積等.如圖,打開軟件后將手機(jī)攝像頭的屏幕準(zhǔn)星對準(zhǔn)腳部按鍵,再對準(zhǔn)頭部按鍵,即可測量出人體的高度.其數(shù)學(xué)原理如圖②所示,測量者AB與被測量者CD都垂直于地面BC.若手機(jī)顯示AC=1m,AD=1.8m,∠CAD=60°,求此時(shí)CD的高.(結(jié)果保留根號)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
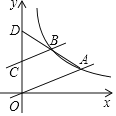
【題目】如圖,在平面直角坐標(biāo)系中,直線![]() 與雙曲線
與雙曲線![]() 交于點(diǎn)A,過點(diǎn)
交于點(diǎn)A,過點(diǎn)![]() 作AO的平行線交雙曲線于點(diǎn)B,連接AB并延長與y軸交于點(diǎn)
作AO的平行線交雙曲線于點(diǎn)B,連接AB并延長與y軸交于點(diǎn)![]() ,則k的值為______.
,則k的值為______.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com