
已知等腰△ABC中,AB=AC,D是BC的中點,將三角板中的90°角的頂點繞D點在△ABC內旋轉,角的兩邊分別與AB、AC交于E、F,且點E、F不與A、B、C三點重合.
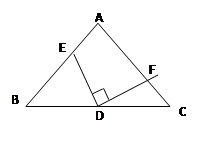
1.如果∠A=90°求證:DE=DF
2.如果DF//AB,則結論:“四邊形AEDF為直角梯形”是否正確,若正確,請證明;若不正確,請畫出草圖舉反例
1.連接AD
∵AB=AC,D是BC的中點,∠A=90°
∴AD=DC, ∠BAD=∠C,
∵∠ADC=90°, ∠EDF=90°
∴∠EDA=∠FDC
∴△ADE≌△CDF 得到DE=DF………………………………4分
2.結論不正確. 圖略 ………………………………1分
反例如下:
取![]() 時,四邊形ADEF為矩形,不是直角梯形。
時,四邊形ADEF為矩形,不是直角梯形。
![]() DF//AB,
DF//AB, ![]()
∴∠AED=90°
當![]() 時,四邊形ADEF為矩形,不是直角梯形。
時,四邊形ADEF為矩形,不是直角梯形。
∴結論不正確………………………………4分
解析:(1)根據等腰直角三角形的性質得到∠C=45°,中線AD平分∠BAC,并且AD=![]() BC,則∠BAD=∠C,AD=DC,又∠EDA=∠CDF,根據全等三角形的判定易得到△ADE≌△CDF,然后根據全等三角形的性質即可得到結論.
BC,則∠BAD=∠C,AD=DC,又∠EDA=∠CDF,根據全等三角形的判定易得到△ADE≌△CDF,然后根據全等三角形的性質即可得到結論.
(2)舉出反例。


 王后雄學案教材完全解讀系列答案
王后雄學案教材完全解讀系列答案 海淀課時新作業金榜卷系列答案
海淀課時新作業金榜卷系列答案科目:初中數學 來源: 題型:
 24、(1)如圖,△ABC紙片中,∠A=36°,AB=AC,請你剪兩刀,分成3張小紙片,使每張小紙片都是等腰三角形.請畫出示意圖,并標明必要的角度;
24、(1)如圖,△ABC紙片中,∠A=36°,AB=AC,請你剪兩刀,分成3張小紙片,使每張小紙片都是等腰三角形.請畫出示意圖,并標明必要的角度;查看答案和解析>>
科目:初中數學 來源: 題型:
| 120 |
| 13 |
| 120 |
| 13 |

查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com