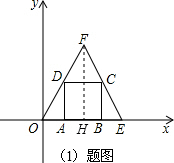
解:(1)如圖,過點(diǎn)F作FH⊥OE于點(diǎn)H,
∵正三角形OEF的邊長為2,
∴OH=

×2=1,
FH=2•sin60°=2×

=

,
∴點(diǎn)F的坐標(biāo)為F(1,

),
又由圖形可得,點(diǎn)O(0,0),E(2,0),
設(shè)過O、E、F三點(diǎn)的拋物線的解析式為y=ax
2+bx+c,
則
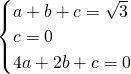
,
解得
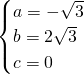
,
所以,拋物線的解析式y(tǒng)=-

x
2+2

x;
(2)方法一:根據(jù)對稱性可得OB=OH+

AB=1+

x,
在矩形ABCD中,AB∥CD,
所以,△FDC∽△FOE,
所以,
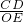
=
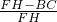
,
即

=

,
解得BC=

-

x,
所以,點(diǎn)C的坐標(biāo)為(1+

x,

-

x),
∵△OEF是等邊三角形,
∴OF與y軸的夾角為30°,
∵點(diǎn)C關(guān)于直線OF的對稱點(diǎn)G恰好落在y軸上,
∴OC與OF的夾角為30°,
∴直線OC與x軸的夾角為30,
tan30°=
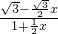
=

,
解得x=1;
方法二:∵△OEF是等邊三角形,
∴OF與y軸的夾角為30°,
∵點(diǎn)C關(guān)于直線OF的對稱點(diǎn)G恰好落在y軸上,
∴OC與OF的夾角為30°,
∵△OEF是等邊三角形,
∴點(diǎn)C是EF的中點(diǎn),
∴CD是△OEF的中位線,
CD=

OE=

×2=1,

∵四邊形ABCD是矩形,
∴AB=CD=1,即x=1;
(3)存在.
理由如下:由(2)可知,OC=2•sin60°=2×

=

,
∵點(diǎn)C、G關(guān)于OF對稱,
∴OG=OC=

,
∴點(diǎn)G的坐標(biāo)為(0,

),
由對稱性可得,OA=

(OE-AB)=

(2-1)=

,
∴點(diǎn)A的坐標(biāo)為(

,0),
①當(dāng)GF∥PA 時(shí),∵F(1,

),
∴GF∥x軸,
∴點(diǎn)P為拋物線與x軸的交點(diǎn),
∴P
1(0,0),P
2(2,0);
②當(dāng)GA∥PF時(shí),∵A(

,0),G(0,

),
∴直線GA的解析式為y=-2

x+

,
∴設(shè)直線PF的解析式為y=-2

x+b,
-2

×1+b=

,
解得b=3

,
所以,直線PF的解析式為y=-2

x+3

,
聯(lián)立

,
解得

,
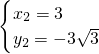
所以,點(diǎn)P的坐標(biāo)為P
3(3,-3

);
③當(dāng)PG∥AF時(shí),A(

,0),F(xiàn)(1,

),
設(shè)直線AF的解析式為y=mx+n,
則
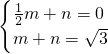
,
解得
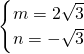
,
所以,直線AF的解析式為y=2

x-

,
所以,設(shè)直線PG的解析式為y=2

x+

,
聯(lián)立
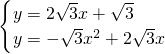
整理得,x
2+1=0,
方程沒有實(shí)數(shù)解,
所以,點(diǎn)P不存在,
綜上得符合條件的點(diǎn)有3個(gè),P
1(0,0),P
2(2,0),P
3(3,-3

).
分析:(1)過點(diǎn)F作FH⊥OE于點(diǎn)H,根據(jù)等邊三角形的性質(zhì)求出HO、HF的長度,然后即可寫出點(diǎn)F的坐標(biāo);再寫出點(diǎn)O、E的坐標(biāo),然后利用待定系數(shù)法求二次函數(shù)解析式解答;
(2)方法一根據(jù)軸對稱性表示出OB的長度,再根據(jù)相似三角形對應(yīng)高的比等于對應(yīng)邊的比列式求出BC的長度,得到點(diǎn)C的坐標(biāo),然后求出OF與y軸的夾角為30°,再根據(jù)對稱性可得∠FOC=30°,從而得到OC與x軸的夾角為30°,根據(jù)30°角的正切值列式求解即可得到x的值;
方法二:先求出OF與y軸的夾角為30°,再根據(jù)軸對稱性可得OC與OF的夾角為30°,然后根據(jù)等邊三角形的性質(zhì)可得點(diǎn)C是EF的中點(diǎn),根據(jù)三角形的中位線定理可得CD=

OE=1,再根據(jù)矩形的對邊相等即可得解;
(3)根據(jù)點(diǎn)C、G關(guān)于OF對稱可得OG=OC,然后求出點(diǎn)G的坐標(biāo),在求出OA的長度得到點(diǎn)A的坐標(biāo),然后分①GF∥PA時(shí),點(diǎn)P是拋物線與x軸的交點(diǎn),即為點(diǎn)O、E的坐標(biāo),②GA∥PF時(shí),先求出直線GA的解析式,再根據(jù)互相平行的兩直線的解析式的k值相等求出直線PF的解析式,與拋物線解析式聯(lián)立求解即可得到點(diǎn)P的坐標(biāo);③PG∥FA時(shí),先求出AF的解析式,再根據(jù)互相平行的兩直線的解析式的k值相等求出直線PG的解析式,與拋物線解析式聯(lián)立可得方程沒有實(shí)數(shù)解.
點(diǎn)評:本題綜合考查了二次函數(shù)的問題,主要利用了等邊三角形的性質(zhì),待定系數(shù)法求二次函數(shù)解析式,相似三角形的判定與性質(zhì),軸對稱的性質(zhì),梯形的兩底邊平行,(3)要注意根據(jù)底邊的不同分情況討論求解.

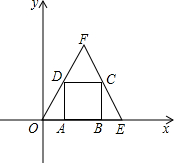 的長為x.
的長為x. 解:(1)如圖,過點(diǎn)F作FH⊥OE于點(diǎn)H,
解:(1)如圖,過點(diǎn)F作FH⊥OE于點(diǎn)H, ×2=1,
×2=1, =
= ,
, ),
),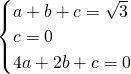 ,
,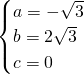 ,
, x2+2
x2+2 x;
x; AB=1+
AB=1+ x,
x,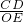 =
=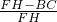 ,
, =
= ,
, -
- x,
x, x,
x, -
- x),
x),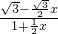 =
= ,
, OE=
OE= ×2=1,
×2=1,
 =
= ,
, ,
, ),
), (OE-AB)=
(OE-AB)= (2-1)=
(2-1)= ,
, ,0),
,0), ),
), ,0),G(0,
,0),G(0, ),
), x+
x+ ,
, x+b,
x+b, ×1+b=
×1+b= ,
, ,
, x+3
x+3 ,
, ,
, ,
,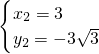
 );
); ,0),F(xiàn)(1,
,0),F(xiàn)(1, ),
),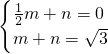 ,
,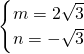 ,
, x-
x- ,
, x+
x+ ,
,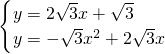 整理得,x2+1=0,
整理得,x2+1=0, ).
). OE=1,再根據(jù)矩形的對邊相等即可得解;
OE=1,再根據(jù)矩形的對邊相等即可得解;



 如圖,在直角坐標(biāo)系中,點(diǎn)P的坐標(biāo)為(3,4),將OP繞原點(diǎn)O逆時(shí)針旋轉(zhuǎn)90°得到線段OP′.
如圖,在直角坐標(biāo)系中,點(diǎn)P的坐標(biāo)為(3,4),將OP繞原點(diǎn)O逆時(shí)針旋轉(zhuǎn)90°得到線段OP′.

 ,2).畫出△ABC的兩個(gè)位似圖形△A1B1C1,△A2B2C2,同時(shí)滿足下列兩個(gè)條件:
,2).畫出△ABC的兩個(gè)位似圖形△A1B1C1,△A2B2C2,同時(shí)滿足下列兩個(gè)條件: