
【題目】某商場銷售一批名牌襯衫,平均每天能售出20件,每件盈利40元。經調查發現:如果這種襯衫的售價每降低1元時,平均每天能多售出2件.設每件襯衫降價x元.
(1)降價后,每件襯衫的利潤為_____元,銷量為_____件;(用含x的式子表示)
(2)為了擴大銷售,盡快減少庫存,商場決定釆取降價措施。但需要平均每天盈利1200元,求每件襯衫應降價多少元?
 七星圖書口算速算天天練系列答案
七星圖書口算速算天天練系列答案 初中學業考試導與練系列答案
初中學業考試導與練系列答案科目:初中數學 來源: 題型:
【題目】電器專營店的經營利潤受地理位置、顧客消費能力等因素的影響,某品牌電腦專營店設有甲、乙兩家分店,均銷售A、B、C、D四種款式的電腦,每種款式電腦的利潤如表1所示.現從甲、乙兩店每月售出的電腦中各隨機抽取所記錄的50臺電腦的款式,統計各種款式電腦的銷售數量,如表2所示.
表1:四種款式電腦的利潤
電腦款式 | A | B | C | D |
利潤(元/臺) | 160 | 200 | 240 | 320 |
表2:甲、乙兩店電腦銷售情況
電腦款式 | A | B | C | D |
甲店銷售數量(臺) | 20 | 15 | 10 | 5 |
乙店銷售數量(臺)8 | 8 | 10 | 14 | 18 |
試運用統計與概率知識,解決下列問題:
(1)從甲店每月售出的電腦中隨機抽取一臺,其利潤不少于240元的概率為 ;
(2)經市場調查發現,甲、乙兩店每月電腦的總銷量相當.現由于資金限制,需對其中一家分店作出暫停營業的決定,若從每臺電腦的平均利潤的角度考慮,你認為應對哪家分店作出暫停營業的決定?并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
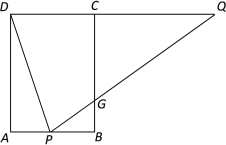
【題目】如圖,矩形ABCD中,AB=4,AD=6,點P在AB上,點Q在DC的延長線上,連接DP,QP,且∠APD=∠QPD,PQ交BC于點G.
(1)求證:DQ=PQ;
(2)求AP·DQ的最大值;
(3)若P為AB的中點,求PG的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
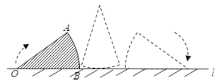
【題目】如圖,在扇形鐵皮AOB中,OA=30,∠AOB=36°,OB在直線l上.將此扇形沿l按順時針方向旋轉(旋轉過程中無滑動),當OA第一次落在l上時,停止旋轉.則點O所經過的路線長為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,二次函數![]() 的圖象與y軸交于C點,交x軸于點A(-2,0),B(6,0),P是該函數在第一象限內圖象上的動點,過點P作PQ⊥BC于點Q,連接PC,AC.
的圖象與y軸交于C點,交x軸于點A(-2,0),B(6,0),P是該函數在第一象限內圖象上的動點,過點P作PQ⊥BC于點Q,連接PC,AC.
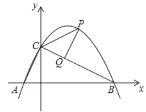
(1)求該二次函數的表達式;
(2)求線段PQ的最大值;
(3)是否存在點P,使得以點P,C,Q為頂點的三角形與△ACO相似?若存在,請求出點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
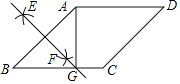
【題目】如圖,在菱形ABCD中,按以下步驟作圖:
①分別以點A和B為圓心,以大于![]() AB的長為半徑作弧,兩弧相交于點E、F;
AB的長為半徑作弧,兩弧相交于點E、F;
②作直線EF交BC于點G,連接AG;若AG⊥BC,CG=3,則AD的長為_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2020年春節聯歡晚會傳承創新亮點多,收視率較往年大幅增長.成都高新區某學校對部分學生就2020年春晚的關注程度,采用隨機抽樣調査的方式,并根據收集到的信息進行統計,繪制了如圖所示的兩幅尚不完整的統計圖(其中A表示“非常關注”;B表示“關注”;C表示“關注很少”;D表示“不關注”).
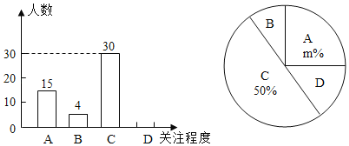
請你根據統計圖中所提供的信息解答下列問題:
(1)直接寫出m=______;估計該校1800名學生中“不關注”的人數是______人;
(2)在一次交流活動中,老師決定從本次調查回答“關注”的同學中隨機選取2名同學來談談他們的想法,而本次調查回答“關注”的這些同學中只有一名男同學,請用畫樹狀圖或列表的方法求選取到兩名同學中剛好有這位男同學的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了解學生對“防溺水”安全知識的掌握情況,從全校1500名學生中隨機抽取部分學生進行測試,并將測試成績(百分制,得分均為整數)進行統計分析,繪制了不完整的頻數表和頻數直方圖.
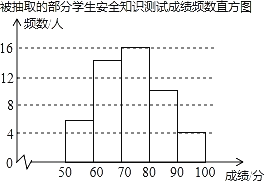
組別 | 成績x(分) | 頻數(人) | 頻率 |
A組 | 50≤x<60 | 6 | 0.12 |
B組 | 60≤x<70 | a | 0.28 |
C組 | 70≤x<80 | 16 | 0.32 |
D組 | 80≤x<90 | 10 | 0.20 |
E組 | 90≤x≤100 | 4 | 0.08 |
由圖表中給出的信息回答下列問題:
(1)表中的a= ;抽取部分學生的成績的中位數在 組;
(2)把如圖的頻數直方圖補充完整;
(3)如果成績達到80分以上(包括80分)為優秀,請估計該校1500名學生中成績優秀的人數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com