
【題目】如圖,平行四邊形ABCD中,AE平分∠BAD,交BC于點E,且AB=AE,延長AB與DE的延長線交于點F.下列結論中:①△ABC≌△AED;②△ABE是等邊三角形;③AD=AF;④S△ABE=S△CDE;⑤S△ABE=S△CEF . 其中正確的是 . 
【答案】①②⑤
【解析】解:∵四邊形ABCD是平行四邊形, ∴AD∥BC,AD=BC,
∴∠EAD=∠AEB,
又∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠BEA,
∴AB=BE,
∵AB=AE,
∴△ABE是等邊三角形;
②正確;
∴∠ABE=∠EAD=60°,
∵AB=AE,BC=AD,
∴△ABC≌△EAD(SAS);
①正確;
∵△FCD與△ABC等底(AB=CD)等高(AB與CD間的距離相等),
∴S△FCD=S△ABC ,
又∵△AEC與△DEC同底等高,
∴S△AEC=S△DEC ,
∴S△ABE=S△CEF;
⑤正確.
若AD與AF相等,即∠AFD=∠ADF=∠DEC
即EC=CD=BE
即BC=2CD,
題中未限定這一條件
∴③④不一定正確;
故答案為:①②⑤.
由平行四邊形的性質得出AD∥BC,AD=BC,由AE平分∠BAD,可得∠BAE=∠DAE,可得∠BAE=∠BEA,得AB=BE,由AB=AE,得到△ABE是等邊三角形,②正確;則∠ABE=∠EAD=60°,由SAS證明△ABC≌△EAD,①正確;由△FCD與△ABD等底(AB=CD)等高(AB與CD間的距離相等),得出S△FCD=S△ABD , 由△AEC與△DEC同底等高,所以S△AEC=S△DEC , 得出S△ABE=S△CEF . ⑤正確.


 狀元坊全程突破導練測系列答案
狀元坊全程突破導練測系列答案 直通貴州名校周測月考直通名校系列答案
直通貴州名校周測月考直通名校系列答案科目:初中數學 來源: 題型:
【題目】計算題:
(1)(﹣1)2012+(π﹣3.14)0﹣(﹣ ![]() )﹣1;
)﹣1;
(2)![]() a2bc3(﹣2a2b2c)2;
a2bc3(﹣2a2b2c)2;![]()
(3)(4a3b﹣6a2b22ab)÷2ab;
(4)x2﹣(x+2)(x﹣2)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司有員工50人,為了提高經濟效益,決定引進一條新的生產線并從現有員工中抽調一部分員工到新的生產線上工作,經調查發現:分工后,留在原生產線上工作的員工每月人均產值提高40%;到新生產線上工作的員工每月人均產值為原來的3倍,設抽調x人到新生產線上工作.
(1)填空:若分工前員工每月的人均產值為a元,則分工后,留在原生產線上工作的員工每月人均產值是元,每月的總產值是元;到新生產線上工作的員工每月人均產值是元,每月的總產值是元;
(2)分工后,若留在原生產線上的員工每月生產的總產值不少于分工前原生產線每月生產的總產值;而且新生產線每月生產的總產值又不少于分工前生產線每月生產的總產值的一半.問:抽調的人數應該在什么范圍?
查看答案和解析>>
科目:初中數學 來源: 題型:
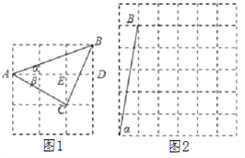
【題目】(1)如圖1,如果ɑ,β都為銳角,且tanɑ=![]() ,tanβ=
,tanβ=![]() ,則ɑ+β=___________;
,則ɑ+β=___________;
(2)如果ɑ,β都為銳角,當tanɑ=5,tanβ=![]() 時,在圖2的正方形網格中,利用已作出的銳角ɑ,畫出∠MON,使得∠MON=ɑ-β.此時ɑ-β=__________度.
時,在圖2的正方形網格中,利用已作出的銳角ɑ,畫出∠MON,使得∠MON=ɑ-β.此時ɑ-β=__________度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,長方形OABC中,O為平面直角坐標系的原點,點A、C的坐標分別為A(3,0),C(0,2),點B在第一象限. 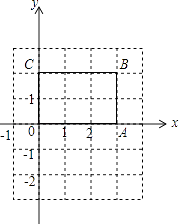
(1)寫出點B的坐標;
(2)若過點C的直線交長方形的OA邊于點D,且把長方形OABC的周長分成2:3的兩部分,求點D的坐標;
(3)如果將(2)中的線段CD向下平移3個單位長度,得到對應線段C′D′,在平面直角坐標系中畫出△CD′C′,并求出它的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】地球上陸地的面積約為150 000 000km2.把“150 000 000”用科學記數法表示為( )
A. 1.5×108 B. 1.5×107 C. 1.5×109 D. 1.5×106
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】根據已知求值.
(1)已知3×9m×27m=316 , 求m的值.
(2)已知am=2,an=5,求a2m﹣3n的值.
(3)已知2x+5y﹣3=0,求4x32y的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com