
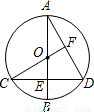
 ∠BOC,則∠C=
∠BOC,則∠C= ∠BOC,根據直角三角形的兩個銳角互余即可求解.
∠BOC,根據直角三角形的兩個銳角互余即可求解.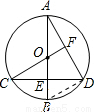 解:方法一:連接BD.
解:方法一:連接BD.  ∠BOC,
∠BOC, ∠BOC.
∠BOC.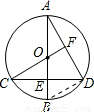 ∵CF⊥AD,AB⊥CD,∠A=∠A,
∵CF⊥AD,AB⊥CD,∠A=∠A, ∠BOC是解題的關鍵.
∠BOC是解題的關鍵. 

 期末寶典單元檢測分類復習卷系列答案
期末寶典單元檢測分類復習卷系列答案科目:初中數學 來源: 題型:
 22、如圖,在⊙O中,直徑AB與弦CD相交于點P,∠CAB=40°,∠APD=65°.
22、如圖,在⊙O中,直徑AB與弦CD相交于點P,∠CAB=40°,∠APD=65°.查看答案和解析>>
科目:初中數學 來源: 題型:
 直線AB相交于點G.
直線AB相交于點G.查看答案和解析>>
科目:初中數學 來源: 題型:
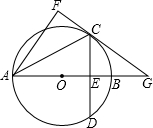 C與直線AB相交于點G.
C與直線AB相交于點G.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com