
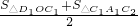 ,S右2=
,S右2=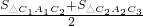 ).
). ?若存在,請求出點P的坐標;若不存在,請說明理由.
?若存在,請求出點P的坐標;若不存在,請說明理由.
 ×2×|x+2|=21,
×2×|x+2|=21, ×2(2n-1+2)=2n+1,
×2(2n-1+2)=2n+1, ×2(2n-2+2+2n+2)=4n+2.
×2(2n-2+2+2n+2)=4n+2. (3)∵以OA1=2為底邊做等腰三角形,∴A1的坐標為:(2,0),
(3)∵以OA1=2為底邊做等腰三角形,∴A1的坐標為:(2,0), ,解得:
,解得: ,
, x2-
x2- x-2,
x-2, ×2×3=6.
×2×3=6. .
. ×4×[x+2-(
×4×[x+2-( x2-
x2- x-2)]=
x-2)]= ×6,
×6, x2-
x2- x-2=-2.
x-2=-2. x2-
x2- x-2=0.
x-2=0. (x+1)[
(x+1)[ +y-5]=
+y-5]= ×6,
×6, x2-
x2- x-8=0,
x-8=0, .
. 時,y=
時,y= x2-
x2- x-2=7+
x-2=7+ .
. 時,y=
時,y= x2-
x2- x-2=7-
x-2=7- .
. ,7+
,7+ ),P4(1-
),P4(1- ,7-
,7- ).
). ,7+
,7+ ),P4(1-
),P4(1- ,7-
,7- ).
). ,然后分兩種情況進行討論:①點P在直線y=x+2的下方,②點P在直線y=x+2的上方.針對這兩種情況,都可以根據△PD1C2的面積是△C1OD1與△C1A1C2面積和的
,然后分兩種情況進行討論:①點P在直線y=x+2的下方,②點P在直線y=x+2的上方.針對這兩種情況,都可以根據△PD1C2的面積是△C1OD1與△C1A1C2面積和的 ,列出方程,解方程即可.
,列出方程,解方程即可.

科目:初中數學 來源: 題型:
 如圖,以點O為位似中心,將五邊形ABCDE放大后得到五邊形A1B1C1D1E1,已知OA=10cm,OA1=20cm,五邊形ABCDE的面積為50cm2,則五邊形A1B1C1D1E1的面積為
如圖,以點O為位似中心,將五邊形ABCDE放大后得到五邊形A1B1C1D1E1,已知OA=10cm,OA1=20cm,五邊形ABCDE的面積為50cm2,則五邊形A1B1C1D1E1的面積為查看答案和解析>>
科目:初中數學 來源: 題型:
| S△D1OC1+S△C1A1C2 |
| 2 |
| S△C1A1C2+S△C2A2C3 |
| 2 |
| 4 |
| 3 |

查看答案和解析>>
科目:初中數學 來源:2012年浙江省杭州市拱墅區下城區中考數學一模試卷(解析版) 題型:解答題
 ,S右2=
,S右2= ).
). ?若存在,請求出點P的坐標;若不存在,請說明理由.
?若存在,請求出點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源:2012年江蘇省無錫市江陰市初級中學中考數學模擬試卷(解析版) 題型:解答題
 ,S右2=
,S右2= ).
). ?若存在,請求出點P的坐標;若不存在,請說明理由.
?若存在,請求出點P的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com