
【題目】規定兩數![]() 之間的一種運算,記作(
之間的一種運算,記作(![]() );如果
);如果![]() ,那么(
,那么(![]() )
)![]() ,例如因為
,例如因為![]() ,所以(2,8)=3.
,所以(2,8)=3.
(1)根據上述規定,填空:(4,16)= ,(7,1)= ,( ,81)=4.
(2)小明在研究這種運算時發現一個現象,(![]() ,
,![]() )=(3,4),小明給出了如下的證明:
)=(3,4),小明給出了如下的證明:
設(![]() ,
,![]() )
)![]() ,所以
,所以![]() ,即
,即![]() ,所以
,所以![]() ,
,
即(3,4)![]() ,所以(
,所以(![]() ,
,![]() )=(3,4),請你嘗試運用這種方法解決下列問題:
)=(3,4),請你嘗試運用這種方法解決下列問題:
①證明:(6,45)-(6,9)=(6,5)
②猜想:(![]() ,
,![]() )+(
)+(![]() ,
,![]() )=( , )(結果化成最簡形式)
)=( , )(結果化成最簡形式)
【答案】(1)2,0,![]() ;(2)①見解析;②
;(2)①見解析;②![]() .
.
【解析】
(1)根據規定的兩數之間的運算法則解答;
(2)①根據同底數冪的乘法法則,結合定義證明;
②根據例題和①中證明的式子作為公式進行變形即可.
解:(1)因為42=16,所以【4,16】=2.
因為70=1,所以【7,1】=0.
因為(±3)4=81,所以【±3,81】=4.
故答案為:2,0,±3;
(2)①證明:設【6,9】=x,【6,5】=y,則6x=9,6y=5,
∴5×9=45=6x6y=6x+y,
∴【6,45】=x+y,
則:【6,45】=【6,9】+【6,5】,
∴【6,45】-【6,9】=【6,5】;
②∵【3n,4n】=【3,4】,
∴【(x+1)m,(y-1)m】
=【(x+1),(y-1)】,【(x+1)n,(y-2)n】
=【(x+1),(y-2)】,
∴【(x+1)m,(y-1)m】+【(x+1)n,(y-2)n】,
=【(x+1),(y-1)】+【(x+1),(y-2)】,
=【(x+1),(y-1)(y-2)】,
=【(x+1),(y2-3y+2)】.
故答案為:(x+1),(y2-3y+2).


科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+bx﹣5與坐標軸交于A(﹣1,0),B(5,0),C(0,﹣5)三點,頂點為D.
(1)請直接寫出拋物線的解析式及頂點D的坐標;
(2)連接BC與拋物線的對稱軸交于點E,點P為線段BC上的一個動點(點P不與B、C兩點重合),過點P作PF∥DE交拋物線于點F,設點P的橫坐標為m.
①是否存在點P,使四邊形PEDF為平行四邊形?若存在,求出點P的坐標;若不存在,說明理由.
②過點F作FH⊥BC于點H,求△PFH周長的最大值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如果任意選擇一對有序整數(m,n),其中|m|≤1,|n|≤3,每一對這樣的有序整數被選擇的可能性是相等的,那么關于x的方程x2+nx+m=0有兩個相等實數根的概率是______.
查看答案和解析>>
科目:初中數學 來源: 題型:
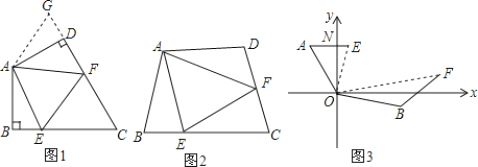
【題目】問題背景:
如圖1,在四邊形ABCD中,AB=AD,∠BAD=120°,∠B=∠D=90°.E、F分別是BC、CD上的點,且∠EAF=60°.為了探究圖中線段BE,EF,FD之間的數量關系,小紅的想法是:在EB的延長線上取一點G,使得BG=DF,連接AG,證明△ABG≌△ADF;再證明△AGE≌△AFE,從而得到結論,她的結論是_____________.
探索延伸:
如圖2,若在四邊形ABCD中,AB=AD,∠B+∠D=180°.E、F分別是BC、CD上的點,且∠EAF=![]() ∠BAD,上述結論是否仍然成立,并說明理由.
∠BAD,上述結論是否仍然成立,并說明理由.
實際應用:
如圖3,在某次軍事演習中,艦艇甲在指揮中心(O處)北偏西40°的A處,艦艇乙在指揮中心南偏東80°的B處,并且兩艦艇到指揮中心的距離相等,接到行動指令后,艦艇甲向正東方向以50海里/小時的速度,同時艦艇乙沿北偏東50°的方向以70海里/小時的速度各自前進2小時后,在指揮中心觀測到甲、乙兩艦艇分別到達E,F處,兩艦艇與指揮中心之間的夾角為70°,則此時兩艦艇之間的距離為______海里.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某倉庫原有商品300件,現記錄了10天內該類商品進出倉庫的件數如下所示(“+”表示進庫,“-”表示出庫)
+30,-10,-15,+25,+17,+35,-20,-15,+13,-35.
(1)請問經過10天之后,該倉庫內的商品是增加了還是減少了?此時倉庫還有多少商品?
(2)如果商品每次進出倉庫需要人工搬運費是每件3元,請問這10天要付多少人工搬運費?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀型綜合題
對于實數![]() 我們定義一種新運算
我們定義一種新運算![]() (其中
(其中![]() 均為非零常數),等式右邊是通常的 四則運算,由這種運算得到的數我們稱之為線性數,記為
均為非零常數),等式右邊是通常的 四則運算,由這種運算得到的數我們稱之為線性數,記為![]() ,其中
,其中![]() 叫做線性數的一個數對.若實數
叫做線性數的一個數對.若實數 ![]() 都取正整數,我們稱這樣的線性數為正格線性數,這時的
都取正整數,我們稱這樣的線性數為正格線性數,這時的![]() 叫做正格線性數的正格數對.
叫做正格線性數的正格數對.
(1)若![]() ,則
,則![]() ,
,![]() ;
;
(2)已知![]() ,
,![]() .若正格線性數
.若正格線性數![]() ,(其中
,(其中![]() 為整數),問是否有滿足這樣條件的正格數對?若有,請找出;若沒有,請說明理由.
為整數),問是否有滿足這樣條件的正格數對?若有,請找出;若沒有,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,△ABC為等邊三角形,點D為AC上的一個動點,點E為BC延長線上一點,且BD=DE.
(1)如圖1,若點D在邊AC上,猜想線段AD與CE之間的關系,并說明理由;
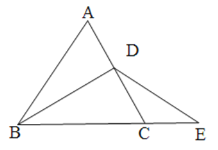
圖1
(2)如圖2,若點D在AC的延長線上,(1)中的結論是否成立,請說明理由.
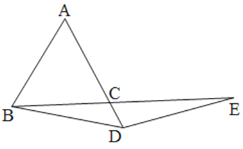
圖2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知反比例函數y1=![]() 的圖象與一次函數y2=ax+b的圖象交于點A(1,4)和點B(m,-2).
的圖象與一次函數y2=ax+b的圖象交于點A(1,4)和點B(m,-2).
(1)求這兩個函數的表達式;
(2)根據圖象直接寫出一次函數的值大于反比例函數的值的x的取值范圍.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平面上有射線AP和點B,C,請用尺規按下列要求作圖:
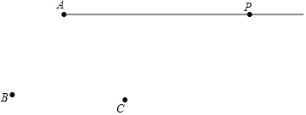
(1)連接AB,并在射線AP上截取AD=AB;
(2)連接BC、BD,并延長BC到E,使BE=BD.
(3)在(2)的基礎上,取BE中點F,若BD=6,BC=4,求CF的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com