
【題目】豐都縣某中學為培養學生綜合實踐能力,開展了一系列綜合實踐活動,有一次財商訓練活動中,小明同學準備去集市批發兩種商品用于活動中交易.預先了解到A、B兩種商品的價格之和為27元,小明計劃購買B商品的數量比A商品的數量多2件,但一共不超過25件,且每樣不少于3件,但小明去購買時發現A商品正打九折銷售,而B商品的價格提高了20%,小明決定將A、B產品的購買數量對調,這樣實際花費只比計劃多8元,已知價格和購買數量均為整數,則小明購買兩種商品實際花費為_____元.
【答案】312.
【解析】
設A商品的單價為x元/件,則B商品的單價為(27﹣x)元/件,計劃購買A商品a件,則B商品為(a+2)件,根據題中等量關系可列出關于x的方程,用含a的式子表示出x,由“一共不超過25件,且每樣不少于3件”“ 價格和購買數量均為整數”可知a的值,易求x的值.
設A商品的單價為x元/件,則B商品的單價為(27﹣x)元/件,計劃購買A商品a件,則B商品為(a+2)件,
根據題意可得:0.9x×(a+2)+1.2×(27﹣x)×a=xa+(27﹣x)(a+2)+8,
∴x=![]() ,
,
∵a≥3,a+2≥3,a+a+2≤25,x,a均為整數,
∴a=10,x=10
∴小明購買兩種商品實際花費=9×12+1.2×10×17=312元,
故答案為:312.


科目:初中數學 來源: 題型:
【題目】如圖,二次函數![]() 的圖象與
的圖象與![]() 軸交于
軸交于![]() 兩點,點
兩點,點![]() 位于
位于![]() 、
、![]() 之間,與
之間,與![]() 軸交于點
軸交于點![]() ,對稱軸為直線
,對稱軸為直線![]() ,直線
,直線![]() 與拋物線
與拋物線![]() 交于
交于![]() 兩點,
兩點,![]() 點在
點在![]() 軸上方且橫坐標小于5,則下列結論:①
軸上方且橫坐標小于5,則下列結論:①![]() ;②
;②![]() ;③
;③![]() (其中
(其中![]() 為任意實數);④
為任意實數);④![]() ,其中正確的是( )
,其中正確的是( )
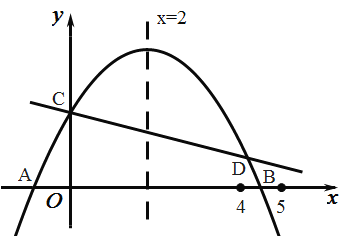
A.①②③④B.①②③C.①②④D.①③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已如拋物線y=ax2+bx+c與直線y=mx+n相交于兩點,這兩點的坐標分別是(0,﹣![]() )和(m﹣b,m2﹣mb+n),其中a,b,c,m,n為實數,且a,m不為0.
)和(m﹣b,m2﹣mb+n),其中a,b,c,m,n為實數,且a,m不為0.
(1)求c的值;
(2)求證:拋物線y=ax2+bx+c與x軸有兩個交點;
(3)當﹣1≤x≤1時,設拋物線y=ax2+bx+c與x軸距離最大的點為P(x0,y0),求這時|y0|的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在水果銷售旺季,某水果店購進一優質水果,進價為20元/千克,售價不低于20元/千克,且不超過32元/千克,根據銷售情況,發現該水果一天的銷售量y(千克)與該天的售價x(元/千克)滿足如下表所示的一次函數關系.
銷售量y(千克) | … | 34.8 | 32 | 29.6 | 28 | … |
售價x(元/千克) | … | 22.6 | 24 | 25.2 | 26 | … |
(1)某天這種水果的售價為23.5元/千克,求當天該水果的銷售量.
(2)如果某天銷售這種水果獲利150元,那么該天水果的售價為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖(1),△ABC和△AOD都是等腰直角三角形,∠BAC=∠EAD=90°,點B在線段AE上,點C在線段AD上,請直接寫出線段BE與線段CD的數量關系與位置關系;
(2)如圖(2),將圖(1)中的△ABC繞點A順時針施轉α(0°<α<360°),那么(1)中線段BE與線段CD的關系是否還成立?如果成立,請你結合圖(2)給出的情形進行證明;如果不成立,說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,拋物線y=ax2+bx+c與x軸交于A(﹣2,0),B(8,0)兩點,與y軸交于點C,且OC=2OA,拋物線的對稱軸x軸交于點D.
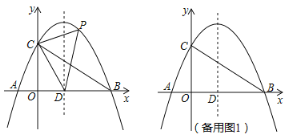
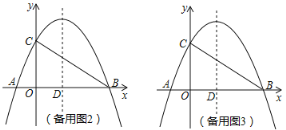
(1)求拋物線的解析式;
(2)點P是第一象限內拋物線上位于對稱軸右側的一個動點,設點P點的橫坐標為m,且S△CDP=![]() S△ABC,求m的值;
S△ABC,求m的值;
(3)K是拋物線上一個動點,在平面直角坐標系中是否存在點H,使B、C、K、H為頂點的四邊形成為矩形?若存在,直接寫出點H的坐標;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,二次函數y=ax2+bx﹣4(a≠0)的圖象與x軸交于點A(﹣2,0)與點C(8,0)兩點,與y軸交于點B,其對稱軸與x軸交于點D.
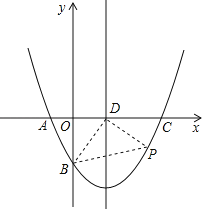
(1)直接寫出B點的坐標;
(2)求該二次函數的解析式;
(3)若點P(m,n)是該二次函數圖象上的一個動點(其中m>0,n<0),連結PB,PD,BD,AB.請問是否存在點P,使得△BDP的面積恰好等于△ADB的面積?若存在請求出此時點P的坐標,若不存在說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為弘揚傳統文化,某校開展了“傳承經典文化,閱讀經典名著”活動.為了解七、八年級學生(七、八年級各有600名學生)的閱讀效果,該校舉行了經典文化知識競賽.現從兩個年級各隨機抽取20名學生的競賽成績(百分制)進行分析,過程如下:
收集數據:
七年級:79,85,73,80,75,76,87,70,75,94,75,79,81,71,75,80,86,59,83,77.
八年級:92,74,87,82,72,81,94,83,77,83,80,81,71,81,72,77,82,80,70,41.
整理數據:
|
|
|
|
|
| |
七年級 | 0 | 1 | 0 | a | 7 | 1 |
八年級 | 1 | 0 | 0 | 7 | b | 2 |
分析數據:
平均數 | 眾數 | 中位數 | |
七年級 | 78 | 75 |
|
八年級 | 78 |
| 80.5 |
應用數據:
(1)由上表填空:a= ,b= ,c= ,d= .
(2)估計該校七、八兩個年級學生在本次競賽中成績在90分以上的共有多少人?
(3)你認為哪個年級的學生對經典文化知識掌握的總體水平較好,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC內接于⊙O,AB是⊙O的直徑,CE平分∠ACB交⊙O于E,交AB于點D,連接AE,∠E=30°,AC=5.
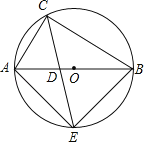
(1)求CE的長;
(2)求S△ADC:S△ACE的比值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com