
【題目】完成下列填空:
(1)如圖,![]() 為直角,
為直角,![]() ,且
,且![]() 平分
平分![]() 平分
平分![]() ,求
,求![]() 的度數.
的度數.
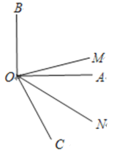
(2)如圖,![]() ,且
,且![]() 平分
平分![]() 平分
平分![]() .直接寫出
.直接寫出![]() 的度數.
的度數.
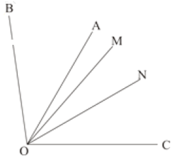
解:(1)因為![]() ,所以
,所以![]() ①
① ![]()
因為![]() 平分
平分![]() ,所以
,所以![]() ②
② ![]() ③
③ ![]()
因為![]() 平分
平分![]() ,所以
,所以![]() ④
④ ![]() ⑤
⑤ ![]()
所以![]() ⑥
⑥ ![]()
(2)![]() ⑦
⑦ ![]()
【答案】①152°;②∠MOC;③76°;④∠NOC;⑤31°;⑥45°;⑦20°
【解析】
(1)結合圖形,根據步驟填寫即可.
(2)先算出∠NOC和∠MOB,再算出∠BON,用∠BON-∠BOM即可得出∠MON.
(1)因為![]() ,所以
,所以![]() ∠AOB+∠AOC=152°,
∠AOB+∠AOC=152°,
因為![]() 平分
平分![]() ,所以∠MOC
,所以∠MOC ![]() 76° ,
76° ,
因為![]() 平分
平分![]() ,所以∠NOC
,所以∠NOC ![]() 31°,
31°,
所以![]() 45°.
45°.
(2)因為∠AOB=40°,∠AOC=58°,所以∠BOC=∠AOB+∠AOC=98°,
因為OM平分∠BOC,所以∠BOM![]() 49°.
49°.
因為ON平分∠AOC,所以∠NOC![]() 29°,所以∠BON=∠BOC-∠NOC=69°,
29°,所以∠BON=∠BOC-∠NOC=69°,
所以∠MON=∠BON-∠BOM=20°.


科目:初中數學 來源: 題型:
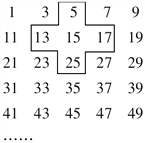
【題目】將連續的奇數1,3,5,7,9,…,排成如圖所示的數陣.
(1)十字框中的五個數的和與中間數15有什么關系?
(2)設中間數為![]() ,求出十字框中五個數之和;
,求出十字框中五個數之和;
(3)十字框中五個數之和能等于2 015嗎?若能,請寫出這五個數;若不能,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC.
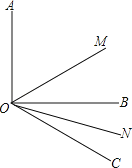
(1)求∠MON的度數;
(2)如果∠AOB=α,其他條件不變,求∠MON的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
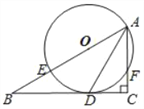
【題目】已知△ABC中∠ACB=90°,E在AB上,以AE為直徑的⊙O與BC相切于D,與AC相交于F,連接AD.
(1)求證:AD平分∠BAC;
(2)連接OC,如果∠B=30°,CF=1,求OC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
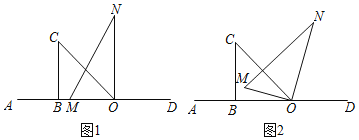
【題目】將一副直角三角板按如圖1擺放在直線AD上![]() 直角三角板OBC和直角三角板MON,
直角三角板OBC和直角三角板MON,![]() ,
,![]() ,
,![]() ,
,![]() ,保持三角板OBC不動,將三角板MON繞點O以每秒
,保持三角板OBC不動,將三角板MON繞點O以每秒![]() 的速度順時針方向旋轉t秒
的速度順時針方向旋轉t秒![]()
![]() 如圖2,
如圖2,![]() ______度
______度![]() 用含t的式子表示
用含t的式子表示![]() ;
;
![]() 在旋轉的過程中,是否存在t的值,使
在旋轉的過程中,是否存在t的值,使![]() ?若存在,請求出t的值;若不存在,請說明理由.
?若存在,請求出t的值;若不存在,請說明理由.
![]() 直線AD的位置不變,若在三角板MON開始順時針旋轉的同時,另一個三角板OBC也繞點O以每秒
直線AD的位置不變,若在三角板MON開始順時針旋轉的同時,另一個三角板OBC也繞點O以每秒![]() 的速度順時針旋轉.
的速度順時針旋轉.
![]() 當
當![]() ______秒時,
______秒時,![]() ;
;
![]() 請直接寫出在旋轉過程中,
請直接寫出在旋轉過程中,![]() 與
與![]() 的數量關系
的數量關系![]() 關系式中不能含
關系式中不能含![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將一張直角三角形紙片![]() 沿斜邊
沿斜邊![]() 上的中線
上的中線![]() 剪開,得到
剪開,得到![]() ,再將
,再將![]() 沿
沿![]() 方向平移到
方向平移到![]() 的位置,若從平移開始到點
的位置,若從平移開始到點![]() 未到達點
未到達點![]() 時,
時,![]() 交
交![]() 于點
于點![]() ,
,![]() 交
交![]() 于點
于點![]() ,連結
,連結![]() .
.
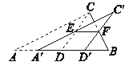
(1)試探究![]() 的形狀,請說明理由;
的形狀,請說明理由;
(2)當四邊形![]() 為菱形時,判斷
為菱形時,判斷![]() 與
與![]() 是否全等,請說明理由.
是否全等,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
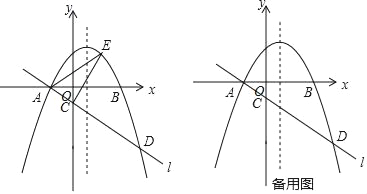
【題目】如圖,在平面直角坐標系中,直線l:y=kx+h與x軸相交于點A(﹣1,0),與y軸相交于點C,與拋物線y=﹣x2+bx+3的一交點為點D,拋物線過x軸上的AB兩點,且CD=4AC.
(1)求直線l和拋物線的解析式;
(2)點E是直線l上方拋物線上的一動點,求當△ADE面積最大時,點E的坐標;
(3)設P是拋物線對稱軸上的一點,點Q在拋物線上,四邊形APDQ能否為矩形?若能,請直接寫出點P的坐標;若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線y=kx+b交x軸于點A(1,0),與雙曲線y=-![]() (x<0)交于點B(-1,a).
(x<0)交于點B(-1,a).
(1)求直線AB的解析式;
(2)若點B左側一直線x=m與直線AB交于點C,與雙曲線交于點D(C、D兩點不重合),當BC=BD時,求m的值.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com