
【題目】小明、小麗兩位同學八年級10次數學單元自我檢測的成績(成績均為整數,且個位數為0)分別如下圖所示:
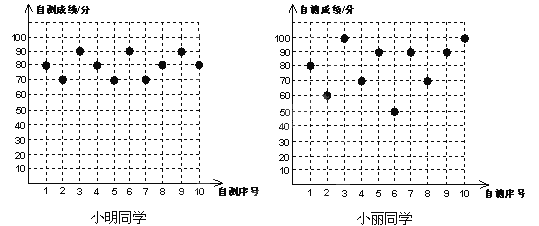
(1)根據上圖中提供的數據填寫下表:
平均成績(分) | 中位數(分) | 眾數(分) | 方差(S2) | |
小明 | 80 | 80 | ||
小麗 | 85 | 260 |
(2)如果將90分以上(含90分)的成績視為優秀,則優秀率高的同學是________;
(3)根據圖表信息,請你對這兩位同學各提一條不超過20個字的學習建議.
【答案】(1)圖表見解析;(2)小麗;(3)小麗同學要提高一下穩定性,小明同學應提高一下最好成績(答案不唯一).
【解析】
(1)由平均數、方差的公式計算平均成績即可;將甲的成績按大小順序排列,中間兩個數的平均數,即為中位數;一組數據中出現次數最多的一個數即為眾數;
(2)比較哪位同學的成績在90分以上(含90分)的成績多,即優秀率高;
(3)比較這兩位同學的方差,方差越小,成績越穩定.
解:(1)小明10次成績分別為:80,70,90,80,70,90,70,80,90,80;
按大小順序排列為:70,70,70,80,80,80,80,90,90,90;
∴中位數是:80,
方差為:![]() =60
=60
小麗10次成績分別為:80,60,100,70,90,50,70,90,70,90;
平均成績為:(80+60+100+70+90+50+70+90+70+90)÷10=80,
眾數是:90
故答案為:
平均成績(分) | 中位數(分) | 眾數(分) | 方差(S2) | |
小明 | 80 | 80 | 80 | 60 |
小麗 | 80 | 85 | 90 | 260 |
(2)小明的優秀率為:![]() ×100%=30%,
×100%=30%,
小麗的優秀率為:![]() ×100%=40%,
×100%=40%,
∴小麗的優秀率高.
故答案為:小麗;
(3)根據方差S小明2<S小麗2,所以小麗同學要提高一下穩定性,根據最大值,小明同學應提高一下最好成績(答案不唯一).


科目:初中數學 來源: 題型:
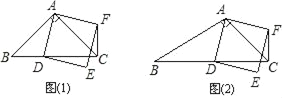
【題目】在△ABC中,∠ACB=45°.點D(與點B、C不重合)為射線BC上一動點,連接AD,以AD為一邊且在AD的右側作正方形ADEF.
(1)如果AB=AC.如圖①,且點D在線段BC上運動.試判斷線段CF與BD之間的位置關系,并證明你的結論.
(2)如果AB≠AC,如圖②,且點D在線段BC上運動.(1)中結論是否成立,為什么?
(3)若正方形ADEF的邊DE所在直線與線段CF所在直線相交于點P,設AC=4![]() ,BC=3,CD=x,求線段CP的長.(用含x的式子表示)
,BC=3,CD=x,求線段CP的長.(用含x的式子表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC是邊長為2的等邊三角形.取BC邊中點E,作ED∥AB,EF∥AC,得到四邊形EDAF,它的面積記作![]() ;取
;取![]() 中點
中點![]() ,作
,作![]() ∥
∥![]() ,
,![]() ∥
∥![]() ,得到四邊形
,得到四邊形![]() ,它的面積記作
,它的面積記作![]() .照此規律作下去,則
.照此規律作下去,則![]() =____________________ .
=____________________ .

查看答案和解析>>
科目:初中數學 來源: 題型:
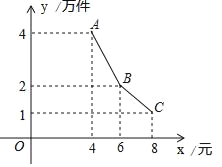
【題目】為了支持大學生創業,某市政府出臺了一項優惠政策:提供10萬元的無息創業貸款.小王利用這筆貸款,注冊了一家淘寶網店,招收5名員工,銷售一種火爆的電子產品,并約定用該網店經營的利潤,逐月償還這筆無息貸款.已知該產品的成本為每件4元,員工每人每月的工資為4千元,該網店還需每月支付其它費用1萬元.該產品每月銷售量y(萬件)與銷售單價x(元)萬件之間的函數關系如圖所示.
(1)求該網店每月利潤w(萬元)與銷售單價x(元)之間的函數表達式;
(2)小王自網店開業起,最快在第幾個月可還清10萬元的無息貸款?
查看答案和解析>>
科目:初中數學 來源: 題型:
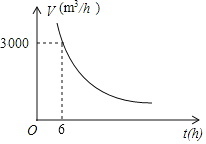
【題目】一蓄水池每小時的排水量V(m3/h)與排完水池中的水所用的時間t(h)之間成反比例函數關系,其圖象如圖所示.
(1)求V與t之間的函數表達式;
(2)若要2h排完水池中的水,那么每小時的排水量應該是多少?
(3)如果每小時排水量不超過4000m3,那么水池中的水至少要多少小時才能排完?
查看答案和解析>>
科目:初中數學 來源: 題型:
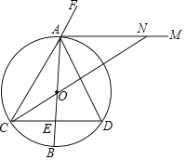
【題目】如圖,AB是⊙O的直徑,弦CD⊥AB于點E,AM是△ACD外角∠DAF的平分線.
(1)求證:AM是⊙O的切線.
(2)若C是優弧ABD的中點,AD=4,射線CO與AM交于N點,求ON的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
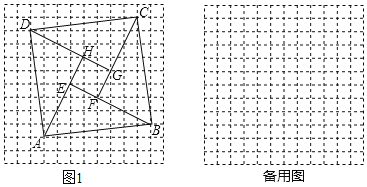
【題目】在每個小正方形的邊長為1的網格圖形中,每個小正方形的頂點稱為格點.以頂點都是格點的正方形ABCD的邊為斜邊,向內作四個全等的直角三角形,使四個直角頂點E,F,G,H都是格點,且四邊形EFGH為正方形,我們把這樣的圖形稱為格點弦圖.例如,在如圖1所示的格點弦圖中,正方形ABCD的邊長為![]() ,此時正方形EFGH的而積為5.問:當格點弦圖中的正方形ABCD的邊長為
,此時正方形EFGH的而積為5.問:當格點弦圖中的正方形ABCD的邊長為![]() 時,正方形EFGH的面積的所有可能值是_____(不包括5).
時,正方形EFGH的面積的所有可能值是_____(不包括5).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:在△ABC中,AB=AC,AD⊥BC于點D,分別過點A和點C作BC、AD邊的平行線交于點E.
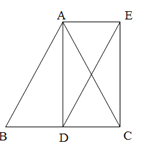
(1)求證:四邊形ADCE是矩形;
(2)連結BE,若![]() ,AD=
,AD=![]() ,求BE的長.
,求BE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某網店銷售一種兒童玩具,進價為每件30元,物價部門規定每件兒童玩具的銷售利潤不高于進價的![]() .在銷售過程中發現,這種兒童玩具每天的銷售量
.在銷售過程中發現,這種兒童玩具每天的銷售量![]() (件
(件![]() 與銷售單價
與銷售單價![]() (元
(元![]() 滿足一次函數關系.當銷售單價為35元時,每天的銷售量為350件;當銷售單價為40元時,每天的銷售量為300件.
滿足一次函數關系.當銷售單價為35元時,每天的銷售量為350件;當銷售單價為40元時,每天的銷售量為300件.
(1)求![]() 與
與![]() 之間的函數關系式.
之間的函數關系式.
(2)當銷售單價為多少時,該網店銷售這種兒童玩具每天獲得的利潤最大,最大利潤是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com