
已知:正方形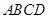 的邊長為1,射線
的邊長為1,射線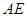 與射線
與射線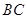 交于點
交于點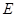 ,射線
,射線 與射線
與射線 交于點
交于點 ,
,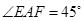 .
.
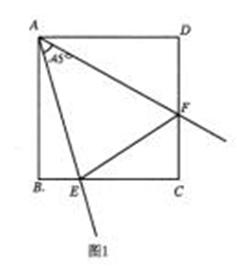
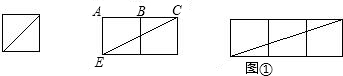
(1)如圖1,當點 在線段
在線段 上時,試猜想線段
上時,試猜想線段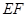 、
、 、
、 有怎樣的數量關系?并證明你的猜想.
有怎樣的數量關系?并證明你的猜想.
(2)設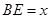 ,
, ,當點
,當點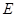 在線段
在線段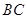 上運動時(不包括點
上運動時(不包括點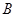 、
、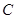 ),如圖 1,求
),如圖 1,求 關于
關于 的函數解析式,并指出
的函數解析式,并指出 的取值范圍.
的取值范圍.
(3)當點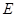 在射線
在射線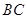 上運動時(不含端點
上運動時(不含端點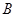 ),點
),點 在射線
在射線 上運動.試判斷以
上運動.試判斷以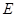 為圓心以
為圓心以 為半徑的
為半徑的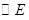 和以
和以 為圓心以
為圓心以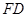 為半徑的
為半徑的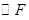 之間的位置關系.
之間的位置關系.

(4)當點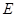 在
在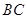 延長線上時,設
延長線上時,設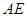 與
與 交于點
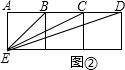
交于點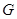 ,如圖 2.問△
,如圖 2.問△ 與△
與△ 能否相似,若能相似,求出
能否相似,若能相似,求出 的值,若不可能相似,請說明理由.
的值,若不可能相似,請說明理由.
(1) 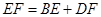 ,證明見解析 (2)
,證明見解析 (2) 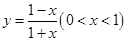 (3) 當點
(3) 當點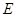 在線段
在線段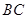 上時,
上時,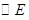 與
與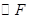 外切;當點
外切;當點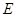 在
在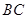 延長線上時,
延長線上時,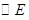 與
與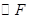 內切.(4)相似,所求
內切.(4)相似,所求 的長為
的長為
【解析】(1)猜想: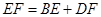 .
(1分)
.
(1分)
 證明:將△
證明:將△ 繞著點
繞著點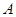 按順時針方向旋轉
按順時針方向旋轉 ,得△
,得△ ,
,
易知點 、
、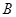 、
、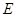 在一直線上.圖1.
(1分)
在一直線上.圖1.
(1分)
∵ ,
,
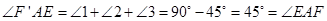 ,
,
又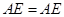 ,
,
∴△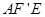 ≌△
≌△
∴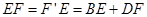 .
(1分)
.
(1分)
(2)由(1)得
又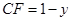 ,
,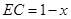 ,
,
∴  (1分)
(1分)
化簡可得 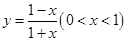 .
(1+1分)
.
(1+1分)
(3)①當點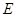 在點
在點 、
、 之間時,由(1)知
之間時,由(1)知 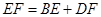 ,故此時
,故此時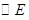 與
與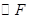 外切;(1分)
外切;(1分)
②當點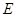 在點
在點 時,
時,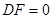 ,
,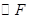 不存在.
不存在.
③當點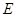 在
在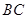 延長線上時,
延長線上時,
將△ 繞著點
繞著點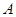 按順時針方向旋轉
按順時針方向旋轉 ,得△
,得△ ,圖2.
,圖2.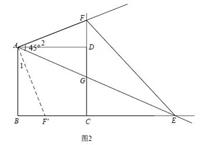
有 ,
, ,
,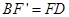 ,
,
∴ .
.
∴ .
.
又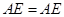 ,
,
∴△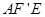 ≌△
≌△ .
(1分)
.
(1分)
∴ .
(1分)
.
(1分)
∴此時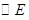 與
與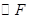 內切.
(1分)
內切.
(1分)
綜上所述,當點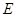 在線段
在線段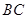 上時,
上時,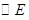 與
與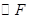 外切;當點
外切;當點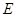 在
在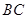 延長線上時,
延長線上時,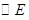 與
與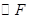 內切.
內切.
(4)△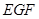 與△
與△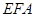 能夠相似,只要當
能夠相似,只要當 即可.
即可.
這時有
 .
(1分)
.
(1分)
設 ,
, ,由(3)有
,由(3)有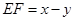
由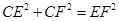 ,得
,得 .
.
化簡可得 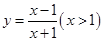 .
(1分)
.
(1分)
又由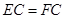 ,得
,得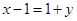 ,即
,即 ,化簡得
,化簡得 , (1分)
, (1分)
解之得, ,
,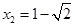 (不符題意,舍去)
(1分)
(不符題意,舍去)
(1分)
∴所求 的長為
的長為 .
.
(1)將△ADF繞著點A按順時針方向旋轉90°,得△ABF′,易知點F′、B、E在一直線上.證得AF′E≌△AFE.從而得到EF=F′E=BE+DF;
(2)由(1)得 EF=x+y再根據 CF=1-y,EC=1-x,得到(1-y)2+(1-x)2=(x+y)2.化簡即可得到y= (0<x<1).
(0<x<1).
(3)當點E在點B、C之間時,由(1)知 EF=BE+DF,故此時⊙E與⊙F外切;當點E在點C時,DF=0,⊙F不存在.當點E在BC延長線上時,將△ADF繞著點A按順時針方向旋轉90°,得△ABF′,證得△AF′E≌△AFE.即可得到EF=EF′=BE-BF′=BE-FD.從而得到此時⊙E與⊙F內切.
(4)△EGF與△EFA能夠相似,只要當∠EFG=∠EAF=45°即可.這時有 CF=CE.設BE=x,DF=y,由(3)有EF=x-y.由 CE2+CF2=EF2,得(x-1)2+(1+y)2=(x-y)2.化簡可得 y= (x>1).又由 EC=FC,得x-1=1+y,即x-1=1+
(x>1).又由 EC=FC,得x-1=1+y,即x-1=1+ ,化簡得x2-2x-1=0,解之即可求得BE的長.
,化簡得x2-2x-1=0,解之即可求得BE的長.


科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
| 2 |

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com