
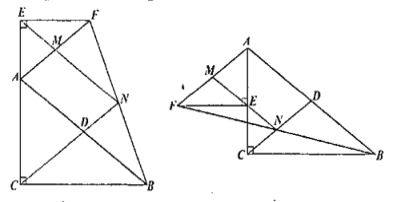
【題目】在![]() 中,
中,![]() ,
,![]() 為斜邊
為斜邊![]() 上的中線;在
上的中線;在![]() 中,
中,![]() ,
,![]() ,且
,且![]() .連接
.連接![]() ,點(diǎn)
,點(diǎn)![]() 、點(diǎn)
、點(diǎn)![]() 分別為線段
分別為線段![]() 的中點(diǎn),連接
的中點(diǎn),連接![]() .
.
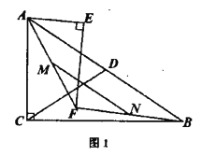
![]() 如圖1,當(dāng)點(diǎn)
如圖1,當(dāng)點(diǎn)![]() 在
在![]() 內(nèi)部時(shí),求證:
內(nèi)部時(shí),求證:![]()
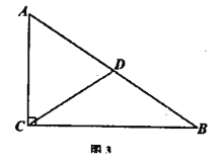
![]() 如圖2,當(dāng)點(diǎn)
如圖2,當(dāng)點(diǎn)![]() 在
在![]() 外部時(shí),連接
外部時(shí),連接![]() ,判斷
,判斷![]() 與
與![]() 的數(shù)量關(guān)系,并加以證明;
的數(shù)量關(guān)系,并加以證明;

![]() 將圖1中的
將圖1中的![]() 繞點(diǎn)
繞點(diǎn)![]() 旋轉(zhuǎn),在旋轉(zhuǎn)的過程中,請直接回答:
旋轉(zhuǎn),在旋轉(zhuǎn)的過程中,請直接回答:
①![]() 中的
中的![]() 與
與![]() 的數(shù)量關(guān)系是否發(fā)生了變化?
的數(shù)量關(guān)系是否發(fā)生了變化?
②若![]() ,當(dāng)點(diǎn)
,當(dāng)點(diǎn)![]() 三點(diǎn)在同一條直線上時(shí),請直摟寫出
三點(diǎn)在同一條直線上時(shí),請直摟寫出![]() 的值.
的值.
【答案】(1)見解析;(2)![]() ;(3)①
;(3)①![]() 與
與![]() 的數(shù)量關(guān)系不變
的數(shù)量關(guān)系不變![]() ;②
;②![]() 或
或![]()
【解析】
(1)利用直角三角形的斜邊的中線等于斜邊的一半和三角形的中位線即可;
(2)根據(jù)三角形的中位線和直角三角形斜邊上的中線等于斜邊的一半可知:![]() 由等邊對等角可知
由等邊對等角可知![]() 再由平行線的性質(zhì)可知
再由平行線的性質(zhì)可知![]() 因此得出:
因此得出:![]() ,所以證得△EMN≌△DNC進(jìn)而得出結(jié)論;
,所以證得△EMN≌△DNC進(jìn)而得出結(jié)論;
(3)①借助(2)得出結(jié)論;
②分兩種情況,如圖,先判斷出點(diǎn)N是以點(diǎn)D為圓心,![]() 為半徑的圓上,即可得出結(jié)論.
為半徑的圓上,即可得出結(jié)論.
(1)證明,在![]() 中
中
![]() 是斜邊
是斜邊![]() 上的中線
上的中線
![]()
在![]() 中,
中,![]() 點(diǎn)
點(diǎn)![]() 分別是邊
分別是邊![]() 的中點(diǎn),
的中點(diǎn),
![]()
![]()
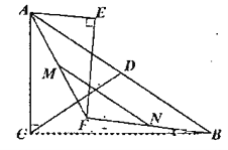
(2)CN與![]() 的數(shù)量關(guān)系是
的數(shù)量關(guān)系是![]()
證明:如圖,連接![]() 。
。
在![]() 中,
中,![]() 是斜邊
是斜邊![]() 上的中線,
上的中線,![]()
![]()
在![]() 中,點(diǎn)
中,點(diǎn)![]() 是斜邊
是斜邊![]() 的中點(diǎn),
的中點(diǎn),
![]()
![]()
![]()
![]()
![]()
![]() 中,點(diǎn)
中,點(diǎn)![]() 、點(diǎn)
、點(diǎn)![]() 、點(diǎn)
、點(diǎn)![]() 分別為線段
分別為線段![]() 的中點(diǎn),
的中點(diǎn),
![]() ,
,
![]()
![]()
![]()
![]()
![]()
即![]()
![]()
![]()
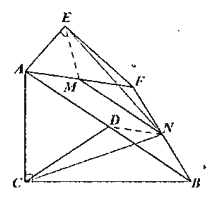
(3)①![]() 與
與![]() 的數(shù)量關(guān)系不變
的數(shù)量關(guān)系不變![]()
與(2)同理可證;
②![]() 或
或![]()
分兩種情況,如圖,
由(2)可知:點(diǎn)N在以點(diǎn)D 為圓心,![]() 為半徑的圓上,
為半徑的圓上,
在Rt△ABC中,CD是AB邊上的中線,
∴CD=![]() AB=
AB=![]() a
a
∵點(diǎn)D、N分別是AB、BF的中點(diǎn),
∴DN=![]() AF=
AF=![]() b
b
∴CN最大=CD+DN=![]() ,CN最小=CD-DN=
,CN最小=CD-DN=![]()
由(2)可知:EN=CN
∴EN最大=![]() ,EN最小=
,EN最小=![]()
∴EN的最大值為![]() ,EN的最小值為
,EN的最小值為![]()
∴EN的值為![]() 或者
或者![]()



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
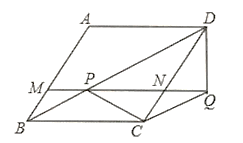
【題目】在菱形![]() 中,
中,![]() ,點(diǎn)
,點(diǎn)![]() 是對角線
是對角線![]() 上一動(dòng)點(diǎn),將線段
上一動(dòng)點(diǎn),將線段![]() 繞點(diǎn)
繞點(diǎn)![]() 順時(shí)針旋轉(zhuǎn)120°到
順時(shí)針旋轉(zhuǎn)120°到![]() ,連接
,連接![]() ,連接
,連接![]() 并延長,分別交
并延長,分別交![]() 于點(diǎn)
于點(diǎn)![]() .
.
(1)求證:![]() ;
;
(2)已知![]() ,若
,若![]() 的最小值為
的最小值為![]() ,求菱形
,求菱形![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
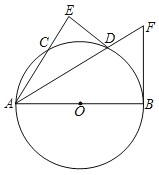
【題目】如圖,AB是直經(jīng),D是![]() 的中點(diǎn),DE⊥AC交AC的延長線于E,⊙O的切線BF交AD的延長線于點(diǎn)F.
的中點(diǎn),DE⊥AC交AC的延長線于E,⊙O的切線BF交AD的延長線于點(diǎn)F.
(1)求證:DE是⊙O的切線.
(2)試探究AE,AD,AB三者之間的等量關(guān)系.
(3)若DE=3,⊙O的半徑為5,求BF的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
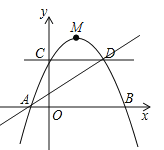
【題目】如圖,已知頂點(diǎn)為![]() 的拋物線過點(diǎn)
的拋物線過點(diǎn)![]() ,交
,交![]() 軸于
軸于![]() 兩點(diǎn),交
兩點(diǎn),交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 是拋物線上一動(dòng)點(diǎn).
是拋物線上一動(dòng)點(diǎn).
![]() 求拋物線的解析式;
求拋物線的解析式;
![]() 當(dāng)點(diǎn)
當(dāng)點(diǎn)![]() 在直線
在直線![]() 上方時(shí),求
上方時(shí),求![]() 面積的最大值,并求出此時(shí)點(diǎn)
面積的最大值,并求出此時(shí)點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
![]() 過點(diǎn)
過點(diǎn)![]() 作直線
作直線![]() 的垂線,垂足為
的垂線,垂足為![]() ,若將
,若將![]() 沿
沿![]() 翻折點(diǎn)
翻折點(diǎn)![]() 的對應(yīng)點(diǎn)為點(diǎn)
的對應(yīng)點(diǎn)為點(diǎn)![]() .是否存在點(diǎn)
.是否存在點(diǎn)![]() ,使
,使![]() 恰好落在
恰好落在![]() 軸上?若存在,求出點(diǎn)
軸上?若存在,求出點(diǎn)![]() 的坐標(biāo):若不存在,說明理由.
的坐標(biāo):若不存在,說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,二次函數(shù)y=ax2+bx+c(a≠0)的圖象與x軸交于點(diǎn)A(-1,0),其對稱軸為直線x=1,下列結(jié)論中正確的是( )
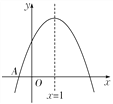
A. abc>0 B. 2a-b=0 C. 4a+2b+c<0 D. 9a+3b+c=0
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,點(diǎn)P在BC上.
(1)求作:△PCD,使點(diǎn)D在AC上,且△PCD∽△ABP;(要求:尺規(guī)作圖,保留作圖痕跡,不寫作法)
(2)在(1)的條件下,若∠APC=2∠ABC,求證:PD//AB.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】為了落實(shí)黨的“精準(zhǔn)扶貧”政策,A、B兩城決定向C,D兩鄉(xiāng)運(yùn)送肥料以支持農(nóng)村生產(chǎn),已知A、B兩城共有肥料500噸,其中A城肥料比B城少100噸,從A城往C、D兩鄉(xiāng)運(yùn)肥料的費(fèi)用分別為20元/噸和25元/噸:從B城往C,D兩鄉(xiāng)運(yùn)肥料的費(fèi)用分別為15元/噸和24元/噸,現(xiàn)C鄉(xiāng)需要肥料240噸,D鄉(xiāng)需要肥料260噸.
(1)A城和B城各有多少噸肥料?
(2)設(shè)從A城運(yùn)往C鄉(xiāng)肥料x噸,總運(yùn)費(fèi)為y元,求y與x的函數(shù)關(guān)系式.
(3)怎樣調(diào)運(yùn)才能使總運(yùn)費(fèi)最少?并求最少運(yùn)費(fèi).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,![]() ,
,![]() ,
,![]() 三點(diǎn)在
三點(diǎn)在![]() 上,直徑
上,直徑![]() 平分
平分![]() ,過點(diǎn)
,過點(diǎn)![]() 作
作![]() 交弦
交弦![]() 于點(diǎn)
于點(diǎn)![]() ,在
,在![]() 的延長線上取一點(diǎn)
的延長線上取一點(diǎn)![]() ,使得
,使得![]() .
.
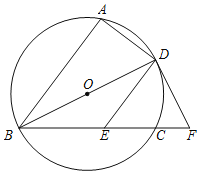
(1)求證:![]() 是
是![]() 的切線;
的切線;
(2)連接AF交DE于點(diǎn)M,若AD=4,DE=5,求DM的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
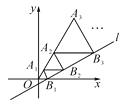
【題目】如圖,在平面直角坐標(biāo)系中,直線l:![]() 與x軸交于點(diǎn)B1,以OB1為邊長作等邊△A1OB1,過點(diǎn)A1作A1B2平行于x軸,交直線l于點(diǎn)B2,以A1B2為邊長作等邊△A2A1B2,過點(diǎn)A2作A2B3平行于x軸,交直線l于點(diǎn)B3,以A2B3為邊長作等邊△A3A2B3,…,則點(diǎn)A2 018的橫坐標(biāo)是_____________.
與x軸交于點(diǎn)B1,以OB1為邊長作等邊△A1OB1,過點(diǎn)A1作A1B2平行于x軸,交直線l于點(diǎn)B2,以A1B2為邊長作等邊△A2A1B2,過點(diǎn)A2作A2B3平行于x軸,交直線l于點(diǎn)B3,以A2B3為邊長作等邊△A3A2B3,…,則點(diǎn)A2 018的橫坐標(biāo)是_____________.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com