分析:(1)要證明△ABC為等邊三角形,證明三邊相等是解答本題的關鍵,將已知三式相加,然后化簡變形,運用因式分解化成完全平方式,根據非負數和為零定理就可以求出a=b=c,從而證明結論.
(2)延長BO1交AC于D,根據內心和等邊三角形的性質可以用字母表示出△ABC的面積及BO1的長度,同樣地方法可以表示出△BB1O1的面積、△BB2O2的面積,依此類推可以表示出△BBnOn的面積.從而求出答案.
解答:(1)證明:∵a
2=b
2+c
2-bc,b
2=a
2+c
2-ac,c
2=a
2+b
2-ab,
∴a
2+b
2+c
2=b
2+c
2-bc+a
2+c
2-ac+a
2+b
2-ab,
∴0=a
2+b
2+c
2-bc-ac-ab,
∴0=2a
2+2b
2+2c
2-2bc-2ac-2ab,
∴0=(a-b)
2+(a-c)
2+(b-c)
2
∴a-b=0,a-c=0,b-c=0
∴a=b,a=c,b=c
∴a=b=c
∴△ABC是等邊三角形;
(2)解:延長BO
1交AC于D

∵O
1為△ABC的內心,
∴BD⊥AC,AD=DC,設AD=x,則AC=2X,在Rt△ABD中由勾股定理,得
BD=
x,
∴S
△ABC=
=4
∴
x
2=4
在Rt△ADO
1中,由勾股定理,得
DO
1=
x∴BO
1=
x
∴EO
1=
x,BE=x
∴S
1=
x
2=
同理可以求出BO
2=
x,O
2F=
x,BF=
x
S
2=
=
x
2=
同理可得:S
3=
…S
n=
∴S
2010=
答:S
1=
,S
2=
,S
2010=
點評:本題考查了三角形的內切圓,因式分解的運用,等邊三角形的判定與性質,勾股定理的運用,三角形面積的計算.

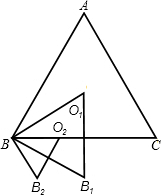
 ∵O1為△ABC的內心,
∵O1為△ABC的內心,

 名校課堂系列答案
名校課堂系列答案 59、已知:三角形ABC內接于⊙O,過點A作直線EF.
59、已知:三角形ABC內接于⊙O,過點A作直線EF.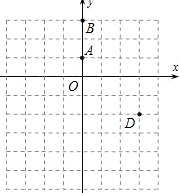 半軸上.關于y軸對稱的拋物線y=ax2+bx+c經過A、D(3,-2)、P三點,且點P關于直線AC的對稱點在x軸上.
半軸上.關于y軸對稱的拋物線y=ax2+bx+c經過A、D(3,-2)、P三點,且點P關于直線AC的對稱點在x軸上. 已知等腰三角形ABC的兩個頂點分別是A(0,1),B(0,3),第三個頂點C在x軸的正半軸上,關于y軸對稱的拋物線y=ax2+bx+c經過點A,D(3,-2).
已知等腰三角形ABC的兩個頂點分別是A(0,1),B(0,3),第三個頂點C在x軸的正半軸上,關于y軸對稱的拋物線y=ax2+bx+c經過點A,D(3,-2). 如圖,正方形網格中的每個小正方形的邊長都是1,每個小正方形的頂點叫做格點.已知直角三角形ABC的三個頂點都在格點上.
如圖,正方形網格中的每個小正方形的邊長都是1,每個小正方形的頂點叫做格點.已知直角三角形ABC的三個頂點都在格點上.