
【題目】小明有5張寫著不同數字的卡片,請你按要求抽出卡片,完成下列各問題:
-3 -5 0 +3 +4
(1)從中取出2張卡片,使這2張卡片上數字的乘積最大,最大乘積是 ;
(2)從中取出2張卡片,使這2張卡片上數字相除的商最小,最小的商是 ;
(3)從中取出4張卡片,用學過的運算方法,使結果為24.寫出運算的式子.(至少寫出兩種)
【答案】(1)15;(2)![]() ;(3)取-3,-5,0,+3,四個數,
;(3)取-3,-5,0,+3,四個數,![]() ;取-3,-5,+3,+4四個數,
;取-3,-5,+3,+4四個數,![]() .
.
【解析】
(1)觀察這五個數,要找乘積最大的就要找符號相同且數值最大的數,所以選-3和-5;
(2)2張卡片上數字相除的商最小就要找符號不同,且分母絕對值越小越好,分子絕對值越大越好,所以就要選3和-5,且-5為分子;
(3)從中取出4張卡片,用學過的運算方法,使結果為24,這就不唯一,用加減乘除只要答數是24即可,比如-3、-5、0、3,四個數,{0-[(-3)+(-5)]}×3=24;再如抽取-3、-5、3、+4,則-[(-3)÷3+(-5)]×4=24.
(1)(-3)×(-5)=15;
(2)(5)÷(+3)=![]() ;
;
(3)方法不唯一,如:抽取3、5、0、+3四個數,則{0[(3)+(5)]}×3=24;
如:抽取3、5、3、4,則[(3)÷3+(5)]×4=24.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】已知:如圖,把△ABC向上平移3個單位長度,再向右平移2個單位長度,得到△A![]() B
B![]() C
C![]() .
.
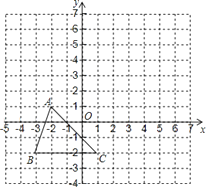
(1)在圖中畫出△A![]() B
B![]() C
C![]() ;
;
(2)寫出點A![]() 、B
、B![]() 、C
、C![]() 的坐標;
的坐標;
(3)在![]() 軸上是否存在一點P,使得△PBC與△ABC面積相等?若存在,寫出點P的坐標;若不存在,說明理由.
軸上是否存在一點P,使得△PBC與△ABC面積相等?若存在,寫出點P的坐標;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,ABCD的對角線AC、BD交于點O,AE平分∠BAD交BC于點E,且∠ADC=60°,AB=![]() BC,連接OE.下列結論:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=
BC,連接OE.下列結論:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=![]() BC,成立的個數有( )
BC,成立的個數有( )

A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
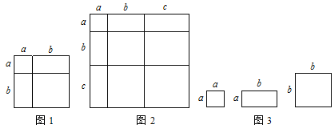
【題目】(知識生成)我們知道,用兩種不同的方法計算同一個幾何圖形的面積,可以得到一些代數恒等式.
例如:如圖可以得到(a+b)2=a2+2ab+b2,基于此,請解答下列問題:
⑴ 根據如圖,寫出一個代數恒等式:
![]() ;
;
⑵ 利用⑴中得到的結論,解決下面的問題:若a+b+c=12,![]() ,
,
則![]() ;
;
⑶ 小明同學用如圖中x張邊長為a的正方形,y張邊長為b的正方形,z張寬、長分別為a、b的長方形紙片拼出一個面積為(2a+b)(a+3b)的長方形,則x+y+z= ;
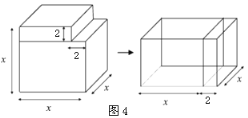
(知識遷移)⑷ 類似地,用兩種不同的方法計算幾何體的體積同樣可以得到一些代數恒等式.如圖表示的是一個邊長為x的正方體挖去一個邊長為2的小長方體后重新拼成一個新長方體.請你根據如圖中兩個圖形的變化關系,寫出一個代數恒等式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,給出以下結論:
①b2>4ac;
②abc>0;
③2a﹣b=0;
④8a+c<0;
⑤9a+3b+c<0,
其中結論正確有( )個。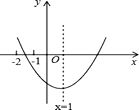
A.2個
B.3個
C.4個
D.5個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場購進甲、乙兩種商品,甲種商品共用了2000元,乙種商品共用了2400元![]() 已知乙種商品每件進價比甲種商品每件進價多8元,且購進的甲、乙兩種商品件數相同.
已知乙種商品每件進價比甲種商品每件進價多8元,且購進的甲、乙兩種商品件數相同.
![]() 求甲、乙兩種商品的每件進價;
求甲、乙兩種商品的每件進價;
![]() 該商場將購進的甲、乙兩種商品進行銷售,甲種商品的銷售單價為60元,乙種商品的銷售單價為88元,銷售過程中發現甲種商品銷量不好,商場決定:甲種商品銷售一定數量后,將剩余的甲種商品按原銷售單價的七折銷售;乙種商品銷售單價保持不變
該商場將購進的甲、乙兩種商品進行銷售,甲種商品的銷售單價為60元,乙種商品的銷售單價為88元,銷售過程中發現甲種商品銷量不好,商場決定:甲種商品銷售一定數量后,將剩余的甲種商品按原銷售單價的七折銷售;乙種商品銷售單價保持不變![]() 要使兩種商品全部售完后共獲利不少于2460元,問甲種商品按原銷售單價至少銷售多少件?
要使兩種商品全部售完后共獲利不少于2460元,問甲種商品按原銷售單價至少銷售多少件?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com