
【題目】如圖,在平面直角坐標系中,拋物線y=ax2+bx﹣3(a≠0)與x軸交于點A(﹣2,0)、B(4,0)兩點,與y軸交于點C.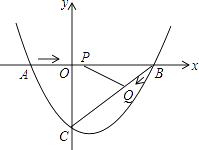
(1)求拋物線的解析式;
(2)點P從A點出發,在線段AB上以每秒3個單位長度的速度向B點運動,同時點Q從B點出發,在線段BC上以每秒1個單位長度的速度向C點運動,其中一個點到達終點時,另一個點也停止運動,當△PBQ存在時,求運動多少秒使△PBQ的面積最大,最大面積是多少?
(3)當△PBQ的面積最大時,在BC下方的拋物線上存在點K,使S△CBK:S△PBQ=5:2,求K點坐標.
【答案】
(1)解:把點A(﹣2,0)、B(4,0)分別代入y=ax2+bx﹣3(a≠0),得
![]() ,
,
解得 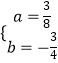 ,
,
所以該拋物線的解析式為:y= ![]() x2﹣
x2﹣ ![]() x﹣3;
x﹣3;
(2)解:設運動時間為t秒,則AP=3t,BQ=t.
∴PB=6﹣3t.
由題意得,點C的坐標為(0,﹣3).
在Rt△BOC中,BC= ![]() =5.
=5.
如圖1,過點Q作QH⊥AB于點H.
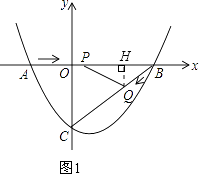
∴QH∥CO,
∴△BHQ∽△BOC,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴HQ= ![]() t.
t.
∴S△PBQ= ![]() PBHQ=
PBHQ= ![]() (6﹣3t)
(6﹣3t) ![]() t=﹣
t=﹣ ![]() t2+
t2+ ![]() t=﹣
t=﹣ ![]() (t﹣1)2+
(t﹣1)2+ ![]() .
.
當△PBQ存在時,0<t<2
∴當t=1時,
S△PBQ最大= ![]() .
.
答:運動1秒使△PBQ的面積最大,最大面積是 ![]() ;
;
(3)解:設直線BC的解析式為y=kx+c(k≠0).
把B(4,0),C(0,﹣3)代入,得
![]() ,
,
解得 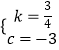 ,
,
∴直線BC的解析式為y= ![]() x﹣3.
x﹣3.
∵點K在拋物線上.
∴設點K的坐標為(m, ![]() m2﹣
m2﹣ ![]() m﹣3).
m﹣3).
如圖2,過點K作KE∥y軸,交BC于點E.則點E的坐標為(m, ![]() m﹣3).
m﹣3).
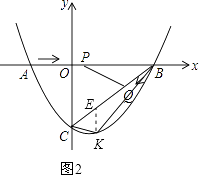
∴EK= ![]() m﹣3﹣(
m﹣3﹣( ![]() m2﹣
m2﹣ ![]() m﹣3)=﹣
m﹣3)=﹣ ![]() m2+
m2+ ![]() m.
m.
當△PBQ的面積最大時,∵S△CBK:S△PBQ=5:2,S△PBQ= ![]() .
.
∴S△CBK= ![]() .
.
S△CBK=S△CEK+S△BEK= ![]() EKm+
EKm+ ![]() EK(4﹣m)
EK(4﹣m)
= ![]() ×4EK
×4EK
=2(﹣ ![]() m2+
m2+ ![]() m)
m)
=﹣ ![]() m2+3m.
m2+3m.
即:﹣ ![]() m2+3m=
m2+3m= ![]() .
.
解得 m1=1,m2=3.
∴K1(1,﹣ ![]() ),K2(3,﹣
),K2(3,﹣ ![]() ).
).
【解析】方法二:(1)略.(2)設運動時間為t秒,則AP=3t,BQ=t,PB=6﹣3t,
∴點C的坐標為(0,﹣3),
∵B(4,0),∴lBC:y= ![]() x﹣3,
x﹣3,
過點Q作QH⊥AB于點H,
∴tan∠HBQ= ![]() ,∴sin∠HBQ=
,∴sin∠HBQ= ![]() ,
,
∵BQ=t,∴HQ= ![]() t,
t,
∴S△PBQ= ![]() PBHQ=
PBHQ= ![]() =﹣
=﹣ ![]() ,
,
∴當t=1時,S△PBQ最大= ![]() .
.
⑶過點K作KE⊥x軸交BC于點E,
∵S△CBK:S△PBQ=5:2,S△PBQ= ![]() ,
,
∴S△CBK= ![]() ,
,
設E(m, ![]() m﹣3),K(m,
m﹣3),K(m, ![]() ),
),
S△CBK= ![]() =
= ![]() =﹣
=﹣ ![]() ,
,
∴﹣ ![]() =
= ![]() ,
,
∴m1=1,m2=3,
∴K1(1,﹣ ![]() ),K2(3,﹣
),K2(3,﹣ ![]() ).
).


科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,AC=BD,E、F、G、H分別是AB、BC、CD、DA的中點,且EG、FH交于點O.若AC=4,則EG2+FH2=______.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖AB是⊙O的直徑,點C為⊙O上一點,AE和過點C的切線互相垂直,垂足為E,AE交⊙O于點D,直線EC交AB的延長線于點P,連接AC,BC,PC=2PB.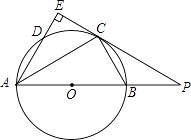
(1)探究線段PB,AB之間的數量關系,并說明理由;
(2)若AD=3,求AB長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,直線l1:y=![]() x與直線l2交點A的橫坐標為2,將直線l1沿y軸向下平移4個單位長度,得到直線l3,直線l3與y軸交于點B,與直線l2交于點C,點C的縱坐標為-2.直線l2與y軸交于點D.
x與直線l2交點A的橫坐標為2,將直線l1沿y軸向下平移4個單位長度,得到直線l3,直線l3與y軸交于點B,與直線l2交于點C,點C的縱坐標為-2.直線l2與y軸交于點D.
(1)求直線l2的解析式;
(2)求△BDC的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AD是BC邊上的高,BE平分∠ABC交AC邊于E,兩線相交于F點.
(1)若∠BAC=60°,∠C=70°,求∠AFB的大小;
(2)若D是BC的中點,∠ABE=30°,求證:△ABC是等邊三角形.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把一副撲克牌中的三張黑桃牌(它們的正面數字分別為3、4、5)洗勻后正面朝下放在桌面上.小王和小李玩摸牌游戲,游戲規則如下:先由小王隨機抽取一張牌,記下牌面數字后放回,洗勻后正面朝下,再由小李隨機抽取一張牌,記下牌面數字.當兩張牌的牌面數字相同時,小王贏;當兩張牌的牌面數字不同時,小李贏.現請你分析游戲規則對雙方是否公平,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知, 四邊形![]() , 連接
, 連接![]() ,
,![]() ,
,![]() .
.
(1)如圖![]() , 求證:
, 求證:![]() 平分
平分![]() ;
;
(2)如圖![]() ,點
,點![]() 在
在![]() 的延長線上,連接
的延長線上,連接![]() 交
交![]() 于點
于點![]() ,求證:
,求證:![]() ;
;
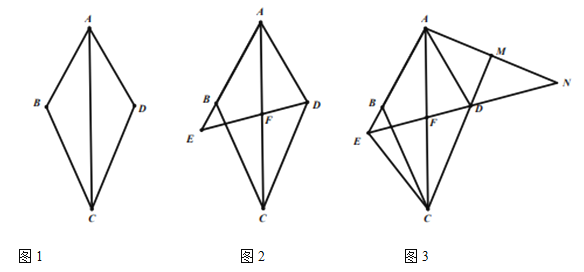
(3)如圖3,在![]() 的條件下,連接
的條件下,連接![]() ,點
,點![]() 在
在![]() 延長線上,連接
延長線上,連接![]() ,延長
,延長![]() 與
與![]() 延長線交于點
延長線交于點![]() , 若
, 若![]() ,
,![]() ,
, ![]() 的面積與
的面積與![]() 的面積比為
的面積比為![]() ,
, ![]() ,
,![]() ,求
,求![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】綜合題
(1)如圖1,銳角△ABC中,AD⊥BC于D,BE⊥AC于E,AD與BE交于F,連DE,求證:DFDA=DBDC;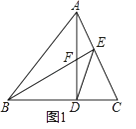
(2)如圖2,若∠BAC=90°,AD⊥BC于D,F為線段AD上一點,在AD延長線上找一點G使AD2=DFDG,請畫出圖形找出點G并加以證明;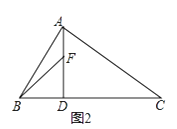
(3)如圖3,在(1)的條件下,若∠ABC=45°,EF=1,EC=3,直接寫出BD長.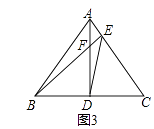
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com