
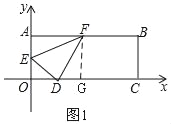
【題目】如圖,平面直角坐標系中,點O為坐標原點,矩形OABC的邊OA,OC在坐標軸上,點B(12,4),點D(3,0),點E(0,2),過點D作DF⊥DE,交AB于點F,連結EF,將△DEF繞點E逆時針方向旋轉,旋轉角度為θ(0°<θ<180°).
(1)求tan∠DFE.
(2)在旋轉過程中,當△DFE的一邊與直線AB平行時,求直線AB截△DFE所得的三角形的面積.
(3)在旋轉過程中,當∠DFE的兩邊所在直線與y軸圍成的三角形為等腰三角形時,求點F的坐標.

【答案】(1)![]() ;(2)見解析;(3)見解析.
;(2)見解析;(3)見解析.
【解析】試題分析:(1)如圖1,作輔助線,構建相似三角形,根據相似比求DG的長,利用勾股定理分別求DE和DF的長,由三角函數定義計算tan∠DFE的值;
(2)分三種情況:
①當ED∥AB時,如圖2,此時直線AB截△DFE所得的三角形是△FGH,
②當DF∥AB時,如圖3,此時直線AB截△DFE所得的三角形是△AGE,
③當EF∥AB時,如圖4,此時直線AB截△DFE所得的三角形是△DGH,
代入面積公式求出面積即可;
(3)分四種情況:
①如圖5,當GF=EF=![]() 時,根據三角函數得:tan∠G=
時,根據三角函數得:tan∠G=![]() ,則
,則![]() ,設FH=a,GH=3a,則GF=
,設FH=a,GH=3a,則GF=![]() a,求出a的值,寫出F的坐標;
a,求出a的值,寫出F的坐標;
②當GF=GE時,如圖6,作輔助線,證明△EFH≌△FED,求FH和OH的長,寫出F的坐標;
③當FG=EF=![]() 時,如圖7,求DG的長,利用勾股定理求EG=
時,如圖7,求DG的長,利用勾股定理求EG=![]() ,利用面積法求FH的長,寫出F的坐標;
,利用面積法求FH的長,寫出F的坐標;
④當EG=EF=![]() 時,如圖8,根據tan∠DFE=tan∠DGE=
時,如圖8,根據tan∠DFE=tan∠DGE=![]() =
=![]() ,設FH=3b,GH=4b,則FG=5b,
,設FH=3b,GH=4b,則FG=5b,
求出b的值,計算OH和FH的長,寫出F坐標.
試題解析:(1)如圖1,過F作FG⊥OC于G,則FG=4,
∵點D(3,0),點E(0,2),
∴OE=2,OD=3,
∵DF⊥DE,
∴∠EDF=90°,
∴∠EDO+∠FDC=90°,
∵∠EOD=90°,
∴∠OED+∠EDO=90°,
∴∠OED=∠FDC,
∵∠EOD=∠FGD=90°,
∴△FDG∽△DEO,
∴![]() ,
,
∴![]() ,
,
∴DG=![]() ,
,
由勾股定理得:DF=![]() =
=![]() =
=![]() ,
,
ED=![]() =
=![]() ,
,
在Rt△DEF中,tan∠DFE=![]() =
=![]() =
=![]() ;
;
(2)分三種情況:
①當ED∥AB時,如圖2,此時直線AB截△DFE所得的三角形是△FGH,
∵DF⊥DE,
∴AB⊥DF,
∴DH=AE=2,
∴FH=DF﹣DH=![]() ﹣2,
﹣2,
由tan∠F=![]() =
=![]() 得:
得: =
=![]() ,
,
∴GH=![]() ,
,
∴S=S△FGH=![]() GHFH=
GHFH=![]() ×
×![]() (
(![]() ﹣2)=
﹣2)=![]() ﹣2
﹣2![]() ;
;

②當DF∥AB時,如圖3,此時直線AB截△DFE所得的三角形是△AGE,
tan∠AEG=![]() =,
=,
∴,
∴AG=,
∴S=S△AGE=AGAE=![]() ×
×![]() ×2=
×2=![]() ;
;

③當EF∥AB時,如圖4,此時直線AB截△DFE所得的三角形是△DGH,
∴∠F=∠DGH,
tan∠F=tan∠DGH=![]() =
=![]() ,
,
設DH=3x,DG=4x,則GH=5x,
過D作DM⊥EF,交GH于N,交EF于M,
∴DN=![]() x,N=AE=2,
x,N=AE=2,
在Rt△DEF中,由勾股定理得:EF=![]() =
=![]() =
=![]() ,
,
S△EDF=![]() DEDF=
DEDF=![]() EFDM,
EFDM,
![]() ×
×![]() =
=![]() ×DM,
×DM,
DM=![]() ,
,
由DN+MN=DM,得:![]() +2=
+2=![]() ,
,
x=![]() ,
,
S=S△DGH=![]() DH×DG=
DH×DG=![]() ×4x×3x=6x2=6×(
×4x×3x=6x2=6×(![]() )2=
)2=![]() ﹣
﹣![]() ;
;

(3)分四種情況:
①如圖5,當GF=EF=![]() 時,
時,
過F作FH⊥y軸于H,則GH=EH,
Rt△GED中,tan∠G=![]() =
=![]() ,
,
∵ED=![]() ,GD=FG+DF=
,GD=FG+DF=![]() +
+![]() =3
=3![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
設FH=a,GH=3a,則GF=![]() a,
a,
∴![]() a=
a=![]()
![]() ,
,
a=![]() ,
,
∴FH=![]() ,
,
OH=OE+HE=2+3×![]() =
=![]() +2=
+2=![]() ,
,
∴F(![]() ,
,![]() );
);

②當GF=GE時,如圖6,
過F作FH⊥y軸于H,
∴∠DFE=∠FEG,
∵∠FHE=∠FDE=90°,EF=EF,
∴△EFH≌△FED,
∴FH=ED=![]() ,HE=DF=
,HE=DF=![]() ,
,
∴OH=EH+OE=![]() +2=
+2=![]() ,
,
∴F(﹣![]() ,
,![]() );
);

③當FG=EF=![]() 時,如圖7,
時,如圖7,
DG=![]() =
=![]() ,
,
Rt△DEG中,
EG=![]() =
=![]() =
=![]() ,
,
過F作FH⊥y軸于H,
∵FG=EF,
∴GH=EH=![]() ,
,
∴OH=![]() +2=
+2=![]() ,
,
S△EGF=![]() GEFH=
GEFH=![]() FGDE,
FGDE,
![]() FH=
FH=![]() ×
×![]() ,
,
![]() FH=
FH=![]() ,
,
FH=![]() ,
,
∴F(﹣![]() ,
,![]() );
);

④當EG=EF=![]()
![]() 時,如圖8,
時,如圖8,
∴∠DFE=∠DGE,
∵ED⊥GF,
∴DF=DG=![]()
![]() ,
,
∴FG=2DF=![]() ,
,
tan∠DFE=tan∠DGE=![]() =
=![]() ,
,
設FH=3b,GH=4b,則FG=5b,
則5b=![]()
![]() ,
,
b=![]()
![]() ,
,
∴FH=3b=3×![]()
![]() =
=![]() ,GH=4b=4×
,GH=4b=4×![]() =
=![]() ,
,
∴OH=OE+EG﹣GH=OE+EF﹣GH=2+![]() ﹣
﹣![]()
![]() =
=![]() ,
,
∴F(﹣![]() ,
,![]() ).
).

綜上所述,點F的坐標為![]() 或
或![]() 或(﹣
或(﹣![]() ,
,![]() )或(﹣
)或(﹣![]() ,
,![]() ).
).


科目:初中數學 來源: 題型:
【題目】(操作發現)如圖1,在邊長為x的正方形內剪去邊長為y的小正方形,剩下的圖形面積可以表示為 ;把剩下的這個圖形沿圖2的虛線剪開,并拼成圖3的長方形,可得長為 、寬為 ,那么這個長方形的面積可以表示為 ,不同的方法求得的面積應相等,由此可以得到一個等式.
(數學應用)利用得到的等式解決以下問題:
(1)![]()
(2)![]()
(思維拓展)(3)利用得到的等式計算![]() …
…![]()
解:原式=![]() …
…![]()
請你把接下來的計算過程補充完整.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,二次函數y=ax2+bx﹣3的圖象與x軸交于A(﹣1,0),點B(4,0),與y軸的交點為C
(1)求二次函數的關系式;
(2)已知點M是線段OB上一動點,過點M作平行于y軸的直線l,直線l與拋物線交于點E,與直線BC交于點F,連接CE,若△CEF與△OBC相似,求點M的坐標;
(3)已知點M是x軸正半軸上一動點,過點M作平行于y軸的直線l,直線l與拋物線交于P,與直線BC交于點Q,連接CP,將△CPQ沿CP翻折后,是否存在這樣的直線l,使得翻折后的點Q剛好落在y軸上?若存在,請求出此時點M的坐標;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某淘寶網店銷售臺燈,每個臺燈售價為60元,每星期可賣出300個,為了促銷,該網店決定降價銷售.市場調查反映:每降價1元,每星期可多賣30個.已知該款臺燈每個成本為40元,
(1)若每個臺燈降x元(![]() ),則每星期能賣出 個臺燈,每個臺燈的利潤是 元.
),則每星期能賣出 個臺燈,每個臺燈的利潤是 元.
(2)在顧客得實惠的前提下,該淘寶網店還想獲得6480元的利潤,應將每件的售價定為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,等邊△A1C1C2的周長為1,作C1D1⊥A1C2于D1,在C1C2的延長線上取點C3,使D1C3=D1C1,連接D1C3,以C2C3為邊作等邊△A2C2C3;作C2D2⊥A2C3于D2,在C2C3的延長線上取點C4,使D2C4=D2C2,連接D2C4,以C3C4為邊作等邊△A3C3C4;…且點A1,A2,A3,…都在直線C1C2同側,如此下去,則△A1C1C2,△A2C2C3,△A3C3C4,…,△AnCnCn+1的周長和為______.(n≥2,且n為整數)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,OC在∠BOD內.
(1)如果∠AOC和∠BOD都是直角.
①若∠BOC=60°,則∠AOD的度數是 ;
②猜想∠BOC與∠AOD的數量關系,并說明理由;
(2)如果∠AOC=∠BOD=x°,∠AOD=y°,求∠BOC的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,點C在線段AB上,AC = 8 cm,CB = 6 cm,點M、N分別是AC、BC的中點.
![]()
(1)求線段MN的長.
(2)若C為線段AB上任意一點,滿足AC+CB=a(cm),其他條件不變,你能猜想出MN的長度嗎?并說明理由.
(3)若C在線段AB的延長線上,且滿足AC-CB=b(cm),M、N分別為AC、BC的中點,你能猜想出MN的長度嗎?請畫出圖形,寫出你的結論,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
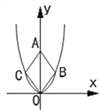
【題目】二次函數y=![]() 的圖象如圖,點O為坐標原點,點A在y軸的正半軸上,點B、C在二次函數y=
的圖象如圖,點O為坐標原點,點A在y軸的正半軸上,點B、C在二次函數y=![]() 的圖象上,四邊形OBAC為菱形,且∠OBA=120°,則菱形OBAC的面積為___________.
的圖象上,四邊形OBAC為菱形,且∠OBA=120°,則菱形OBAC的面積為___________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com