
【題目】邊長相等的下列兩種正多邊形的組合,不能作平面鑲嵌的是( )
A.正方形與正三角形B.正五邊形與正三角形
C.正六邊形與正三角形D.正八邊形與正方形
【答案】B
【解析】
分別求出各個正多邊形每個內角的度數,再結合鑲嵌的條件即可作出判斷.
解:A.正三角形的每個內角是60°,正方形的每個內角是90°,∵3×60°+2×90°=360°,能作平面鑲嵌.
B.正三角形的每個內角是60°,正五邊形每個內角是180°-360°÷5=108°,60m+108n=360°,m=6-![]() n,顯然n取任何正整數時,m不能得正整數,故不能作平面鑲嵌.
n,顯然n取任何正整數時,m不能得正整數,故不能作平面鑲嵌.
C.正三角形的每個內角是60°,正六邊形的每個內角是120°,∵2×60°+2×120°=360°,能作平面鑲嵌.
D.正八邊形的每個內角是135°,正方形的每個內角是90°,∵2×135°+90°=360°,能作平面鑲嵌.
故選:B.


科目:初中數學 來源: 題型:
【題目】問題探究:
(1)如圖①所示是一個半徑為![]() ,高為4的圓柱體和它的側面展開圖,AB是圓柱的一條母線,一只螞蟻從A點出發沿圓柱的側面爬行一周到達B點,求螞蟻爬行的最短路程.(探究思路:將圓柱的側面沿母線AB剪開,它的側面展開圖如圖①中的矩形
,高為4的圓柱體和它的側面展開圖,AB是圓柱的一條母線,一只螞蟻從A點出發沿圓柱的側面爬行一周到達B點,求螞蟻爬行的最短路程.(探究思路:將圓柱的側面沿母線AB剪開,它的側面展開圖如圖①中的矩形![]() 則螞蟻爬行的最短路程即為線段
則螞蟻爬行的最短路程即為線段![]() 的長)
的長)
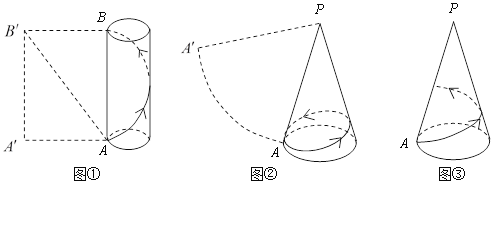
(2)如圖②所示是一個底面半徑為![]() ,母線長為4的圓錐和它的側面展開圖,PA是它的一條母線,一只螞蟻從A點出發沿圓錐的側面爬行一周后回到A點,求螞蟻爬行的最短路程.
,母線長為4的圓錐和它的側面展開圖,PA是它的一條母線,一只螞蟻從A點出發沿圓錐的側面爬行一周后回到A點,求螞蟻爬行的最短路程.
(3)如圖③所示,在②的條件下,一只螞蟻從A點出發沿圓錐的側面爬行一周到達母線PA上的一點,求螞蟻爬行的最短路程.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數![]() 圖象
圖象![]() 軸上方的部分沿
軸上方的部分沿![]() 軸翻折到
軸翻折到![]() 軸下方,圖象的其余部分保持不變,翻折后的圖象與原圖象
軸下方,圖象的其余部分保持不變,翻折后的圖象與原圖象![]() 軸下方的部分組成一個“
軸下方的部分組成一個“![]() ”形狀的新圖象,若直線
”形狀的新圖象,若直線![]() 與該新圖象有兩個公共點,則
與該新圖象有兩個公共點,則![]() 的取值范圍為_____.
的取值范圍為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點M為拋物線![]() 與x軸的焦點為A(-3,0),B(1,0),與y軸交于點C,連結AM,AC,點D為線段AM上一動點(不與A重合),以CD為斜邊在CD上側作等腰Rt△DEC,連結AE,OE.
與x軸的焦點為A(-3,0),B(1,0),與y軸交于點C,連結AM,AC,點D為線段AM上一動點(不與A重合),以CD為斜邊在CD上側作等腰Rt△DEC,連結AE,OE.
(1)求拋物線的解析式及頂點M的坐標;
(2)求解AD:OE的值;
(3)當△OEC為直角三角形時,求AD的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在正方形網格上有6個三角形:①△ABC;②△BCD;③△BDE;④△BFG;⑤△FGH;⑥△EFK.其中②~⑥中與①相似的是( )

A. ②③④ B. ③④⑤ C. ④⑤⑥ D. ②③⑥
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2017年5月,某縣突降暴雨,造成山體滑坡,橋梁垮塌,房屋大面積受損,該省民政廳急需將一批帳篷送往災區.現有甲、乙兩種貨車,已知甲種貨車比乙種貨車每輛車多裝20件帳篷,且甲種貨車裝運1 000件帳篷與乙種貨車裝運800件帳篷所用車輛相等.
(1)求甲、乙兩種貨車每輛車可裝多少件帳篷;
(2)如果這批帳篷有1 490件,用甲、乙兩種汽車共16輛裝運,甲種車輛剛好裝滿,乙種車輛最后一輛只裝了50件,其余裝滿,求甲、乙兩種貨車各有多少輛.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,△ABE和△CDF為直角三角形,∠AEB=∠CFD=90°,AE=CF=5,BE=DF=12,則EF的長是( )

A. 7 B. 8 C. 7![]() D. 7
D. 7![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示△ABC,AB=AC,AD⊥BC,點E、F分別是AB、AC的中點.

(1)求證:四邊形AEDF是菱形;
(2)若四邊形AEDF的周長為12,兩條對角線的和等于7,四邊形AEDF的面積記為S1,三 角形ABC的面積記為S2,S1與S2有何數量關系_____.(直接填答案)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com