
【題目】如圖,在△ABC中,AB=AC=4,P為BC邊上任意一點.
(1)求證:AP2+PB·PC=16.
(2)若BC邊上有100個不同的點(不與點B,C重合)P1,P2,…,P100,設mi=APi2+PiB·PiC(i=1,2,…,100).求m1+m2+…+m100的值.
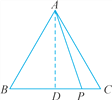
【答案】(1)16;(2)1600
【解析】試題分析:(1)作AD⊥BC于D,由等腰三角形的三線合一性質和勾股定理得出AP2+BPPC=AB2即可;
(2)根據勾股定理,得APi2=AD2+DPi2=AD2+(BD-BPi)2=AD2+BD2-2BDBPi+BPi2,PiBPiC=PiB(BC-PiB)=2BDBPi-BPi2,從而求得mi=AD2+BD2,即可求解.
試題解析:
(1)過點A作AD⊥BC于點D.
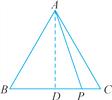
∵AB=AC,AD⊥BC,
∴BD=CD,∠ADB=∠ADC=90°,
∴AP2+PB·PC=AP2+(PD+BD)(CD-PD)=AP2+CD2-PD2.
∵AP2-PD2=AD2,
∴AP2+PB·PC=AD2+CD2=AC2=16.
(2)由(1)知mi=APi2+PiB·PiC=16,
∴m1=m2=…=m100=16,
∴m1+m2+…+m100=16×100=1600.


 快樂小博士鞏固與提高系列答案
快樂小博士鞏固與提高系列答案科目:初中數學 來源: 題型:
【題目】某校計劃開設4門選修課:音樂、繪畫、體育、舞蹈,學校采取隨機抽樣的方法進行問卷調查(每個被調查的學生必須選擇而且只能選擇其中一門),對調查結果進行統計后,繪制了如下不完整的兩個統計圖.

根據以上統計圖提供的信息,回答下列問題:
(1)此次調查抽取的學生人數為a= 人,其中選擇“繪畫”的學生人數占抽樣人數的百分比為b= ;
(2)補全條形統計圖;
(3)若該校有2000名學生,請估計全校選擇“繪畫”的學生大約有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,點A,B的坐標分別為(1,0),(0,2),某拋物線的頂點坐標為D(﹣1,1)且經過點B,連接AB,直線AB與此拋物線的另一個交點為C,則S△BCD:S△ABO=( )
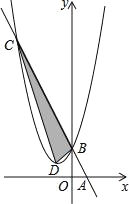
A.8:1 B.6:1 C.5:1 D.4:1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2012年5月某日我國部分城市的最高氣溫統計如下表所示:
城 市 | 武漢 | 成都 | 北京 | 上海 | 海南 | 南京 | 拉薩 | 深圳 |
氣溫(℃) | 27 | 27 | 24 | 25 | 28 | 28 | 23 | 26 |
請問這組數據的平均數是( )
A.24 B.25 C.26 D.27
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com