
【題目】如圖,給出下列四組條件:①AB=DE,BC=EF,AC=DF; ②AB=DE,∠B=∠E,BC=EF;③∠B=∠E,BC=EF,∠C=∠F; ④AB=DE,AC=DF,∠B=∠E.能使△ABC≌△DEF有_____組.

科目:初中數學 來源: 題型:
【題目】已知蝸牛從![]() 點出發,在一條數軸上來回爬行,規定:向正半軸運動記作“+”,向負半軸運動記作“-”,從開始到結束爬行的各段路程(單位:
點出發,在一條數軸上來回爬行,規定:向正半軸運動記作“+”,向負半軸運動記作“-”,從開始到結束爬行的各段路程(單位:![]() )依次為:+7,-5,-10,-8,+9,-6,+12,+4.
)依次為:+7,-5,-10,-8,+9,-6,+12,+4.
(1)若![]() 點在數軸上表示的數為-3,則蝸牛停在數軸上何處,請通過計算加以說明;
點在數軸上表示的數為-3,則蝸牛停在數軸上何處,請通過計算加以說明;
(2)蝸牛在(1)題在數軸上停的位置作以下運動:第1次向左移動1個單位長度至![]() 點,第2次從
點,第2次從![]() 點向右移動2個單位長度至
點向右移動2個單位長度至![]() 點,第3次從
點,第3次從![]() 點向左移動3個單位長度至
點向左移動3個單位長度至![]() 點,第4次從
點,第4次從![]() 點向右移動4個單位長度至
點向右移動4個單位長度至![]() 點,…,依此類推.這樣第2019次移動到的點在數軸上表示的數為(請直接寫出答案).
點,…,依此類推.這樣第2019次移動到的點在數軸上表示的數為(請直接寫出答案).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,CA=CB=5,AB=6,AB⊥y軸,垂足為A.反比例函數y=![]() (x>0)的圖象經過點C,交AB于點D.
(x>0)的圖象經過點C,交AB于點D.
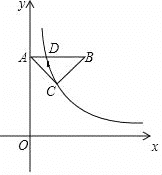
(1)若OA=8,求k的值;
(2)若CB=BD,求點C的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,∠A=160°.第一步:在△ABC上方確定一點A1,使∠A1BA=∠ABC,∠A1CA=∠ACB,如圖1,則∠A1的度數為__;第二步:在△A1BC上方確定一點A2,使∠A2BA1=∠A1BA,∠A2CA1=∠A1CA,如圖2.照此下去,至多能進行___步.
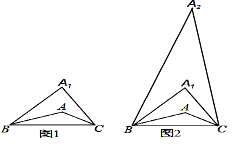
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點O是等邊△ABC內一點,D是△ABC外的一點,∠AOB=110°,∠BOC=α,△BOC≌△ADC,∠OCD=60°,連接OD.
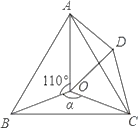
(1)求證:△OCD是等邊三角形;
(2)當α=150°時,試判斷△AOD的形狀,并說明理由;
(3)探究:當α為多少度時,△AOD是等腰三角形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司根據市場計劃調整投資策略,對A、B兩種產品進行市場調查,收集數據如下表:
項目 產品 | 年固定成本 (單位:萬元) | 每件成本 (單位:萬元) | 每件產品銷售價 (萬元) | 每年最多可生產的件數 |
A | 20 | m | 10 | 200 |
B | 40 | 8 | 18 | 120 |
其中,m是待定系數,其值是由生產A的材料的市場價格決定的,變化范圍是6≤m<8,銷售B產品時需繳納![]() x2萬元的關稅.其中,x為生產產品的件數.假定所有產品都能在當年售出,設生產A,B兩種產品的年利潤分別為y1、y2(萬元).
x2萬元的關稅.其中,x為生產產品的件數.假定所有產品都能在當年售出,設生產A,B兩種產品的年利潤分別為y1、y2(萬元).
(1)寫出y1、y2與x之間的函數關系式,注明其自變量x的取值范圍.
(2)請你通過計算比較,該公司生產哪一種產品可使最大年利潤更大?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=mx2﹣6mx+5m與x軸交于A、B兩點,以AB為直徑的⊙P經過該拋物線的頂點C,直線l∥ x軸,交該拋物線于M、N兩點,交⊙ P與E、F兩點,若EF=2![]() ,則MN的長是_____.
,則MN的長是_____.
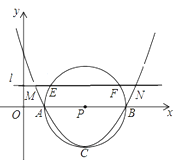
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面的情境對話,然后解答問題

(1)根據“奇異三角形”的定義,請你判斷小華提出的命題:“等邊三角形一定是奇異三角形”是真命題還是假命題?
(2)在Rt![]() ABC 中, ∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若Rt
ABC 中, ∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若Rt![]() ABC是奇異三角形,求a:b:c;
ABC是奇異三角形,求a:b:c;
(3)如圖,AB是⊙O的直徑,C是上一點(不與點A、B重合),D是半圓的中點,CD在直徑AB的兩側,若在⊙O內存在點E使得AE=AD,CB=CE.
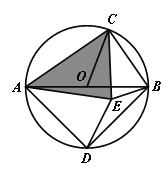
求證:![]() ACE是奇異三角形;
ACE是奇異三角形;
當![]() ACE是直角三角形時,求∠AOC的度數.
ACE是直角三角形時,求∠AOC的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】元旦放假時,小明一家三口一起乘小轎車去探望爺爺、奶奶和姥爺、姥姥.早上從家里出發,向東走了5千米到超市買東西,然后又向東走了2.5千米到爺爺家,下午從爺爺家出發向西走了10千米到姥爺家,晚上返回家里.
(1)若以小明家為原點,向東為正方向,用1個單位長度表示1千米,請將超市、爺爺家和姥爺家的位置在下面數軸上分別用點A、B、C表示出來;
![]()
(2)超市和姥爺家相距多少千米?
(3)若小轎車每千米耗油0.08升,求小明一家從出發到返回家,小轎車的耗油量.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com