
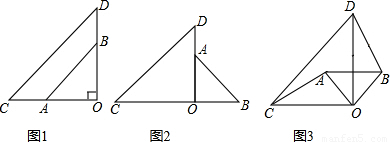
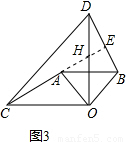
 解:(1)∵△OAB和△OCD都是等腰直角三角形,且疊放在一起,
解:(1)∵△OAB和△OCD都是等腰直角三角形,且疊放在一起,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源:2012屆江蘇省初三第一學期期中考試數學試卷 題型:解答題
如圖甲,兩個不全等的等腰直角三角形OAB和OCD疊放在一起,并且有公共的直角頂點O.
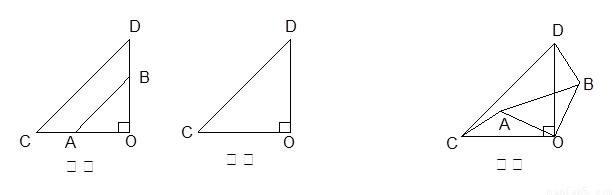
1.在圖甲中,你發現線段AC、BD的數量關系是_______,直線AC、BD相交成____度角
2.將圖甲中的 繞點O順時針旋轉
繞點O順時針旋轉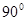 ,在圖乙中作出旋轉后的
,在圖乙中作出旋轉后的 ;
;
3.將圖甲中的 繞點O順時針旋轉一個銳角,得到圖丙,這時(1)中的兩個結論是否成立?作出判斷,并說明理由.若
繞點O順時針旋轉一個銳角,得到圖丙,這時(1)中的兩個結論是否成立?作出判斷,并說明理由.若 繞點O繼續旋轉更大的角度時,結論仍然成立嗎?作出判斷,不必說明理由.
繞點O繼續旋轉更大的角度時,結論仍然成立嗎?作出判斷,不必說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com