Question

等腰三角形的底角為15°，腰長為10，則三角形的面積為    ．

Answer 1

【答案】分析：作一腰上的高．則高和另一腰組成了一個30°的直角三角形，從而求出高和面積．
解答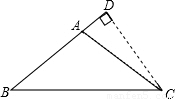：解：如圖，△ABC是等腰三角形，∠ABC=15°，AB=AC=10，
作CD⊥AB交BA延長線于D，
∴∠A=180°-2∠B=150°
∴∠CAD=30°
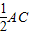
∴CD==5
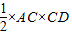
∴三角形的面積為=25．
點評：此題注意畫一個鈍角的等腰三角形，此時腰上的高在三角形的外部．根據等腰三角形的兩個底角相等以及三角形的外角的性質，得到與頂角相鄰的外角是30°，再進一步根據直角三角形的性質計算其高．