
如圖,長方形 中,
中, cm,
cm,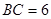 cm,現有一動點
cm,現有一動點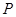 從
從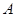 出發以2cm/秒的速度,沿矩形的邊
出發以2cm/秒的速度,沿矩形的邊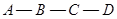 回到點
回到點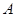 ,設點
,設點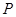 運動的時間為
運動的時間為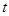 秒.
秒.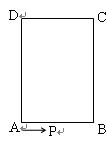
(1)當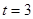 秒時,求
秒時,求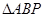 的面積;
的面積;
(2)當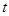 為何值時,點
為何值時,點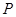 與點
與點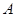 的距離為5cm?
的距離為5cm?
(3)當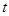 為何值時
為何值時 ,以線段
,以線段 、
、 、
、 的長度為三邊長的三角形是直角三角形,且
的長度為三邊長的三角形是直角三角形,且 是斜邊.
是斜邊.
(1)當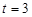 時,點
時,點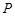 的路程為
的路程為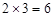 cm …………………(1分)
cm …………………(1分)
∵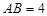 cm,
cm,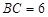 cm
cm
∴點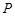 在
在 上
上
∴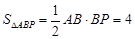 ………………………………(3分)
………………………………(3分)
(2)
(Ⅰ)若點 在
在 上
上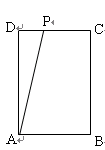
∵在Rt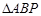 中,
中,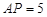 ,
,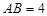
∴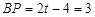
∴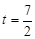 …………………………………………………(5分)
…………………………………………………(5分)
(Ⅱ)若點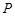 在
在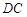 上,則在Rt
上,則在Rt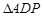 中,
中,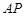 是斜邊
是斜邊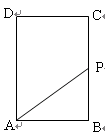
∵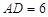 ∴
∴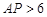 ∴
∴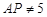 ……………(6分)
……………(6分)
(Ⅲ)若點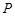 在
在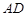 上,
上,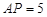
則點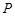 的路程為
的路程為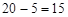
∴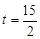 ………………………………………………(8分)
………………………………………………(8分)
綜上,當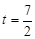 秒或
秒或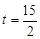 時,
時,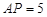 cm. ……………(9分)
cm. ……………(9分)
(3)當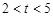 時,點
時,點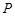 在
在 邊上
邊上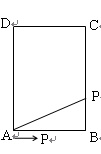
∵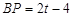 ,
, …………………………(10分)
…………………………(10分)
∴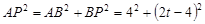
由題意,有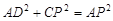
∴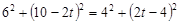
∴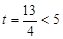 ……………………………………………(12分)
……………………………………………(12分)
解析試題分析:(1)首先算出P點經過的路程,然后P點在BC上,然后利用直角三角形的面積公式求出結果;
(2)分點P在AB、DC、AD邊三種情況進行討論;
(3)首先確定P 點在BC邊上,然后利用勾股定理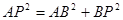 列出方程,然后根據二次函數的性質求出t的值.
列出方程,然后根據二次函數的性質求出t的值.
考點:勾股定理;二次函數性質.
點評:此題要求對P點所經過的位置進行分析討論,然后運用勾股定理計算.


科目:初中數學 來源: 題型:
| 1 | 3 |

查看答案和解析>>
科目:初中數學 來源:2012年初中畢業升學考試(四川成都卷)數學(帶解析) 題型:填空題
如圖,長方形紙片ABCD中,AB=8cm,AD=6cm,按下列步驟進行裁剪和拼圖:
第一步:如圖①,在線段AD上任意取一點E,沿EB,EC剪下一個三角形紙片EBC(余下部分不再使用);
第二步:如圖②,沿三角形EBC的中位線GH將紙片剪成兩部分,并在線段GH上任意取一點M,線段BC上任意取一點N,沿MN將梯形紙片GBCH剪成兩部分;
第三步:如圖③,將MN左側紙片繞G點按順時針方向旋轉180°,使線段GB與GE重合,將MN右側紙片繞H點按逆時針方向旋轉180°,使線段HC與HE重合,拼成一個與三角形紙片EBC面積相等的四邊形紙片.
(注:裁剪和拼圖過程均無縫且不重疊)
則拼成的這個四邊形紙片的周長的最小值為________cm,最大值為________cm.
查看答案和解析>>
科目:初中數學 來源:2012-2013學年福建泉州第三中學八年級上學期期中考試數學試題(解析版) 題型:解答題
如圖,長方形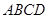 中,
中,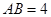 cm,
cm,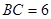 cm,現有一動點
cm,現有一動點 從
從 出發以2cm/秒的速度,沿矩形的邊
出發以2cm/秒的速度,沿矩形的邊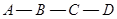 回到點
回到點 ,設點
,設點 運動的時間為
運動的時間為 秒.
秒.

(1)當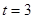 秒時,求
秒時,求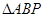 的面積;
的面積;
(2)當 為何值時,點
為何值時,點 與點
與點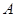 的距離為5cm?
的距離為5cm?
(3)當 為何值時
為何值時 ,以線段
,以線段 、
、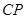 、
、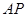 的長度為三邊長的三角形是直角三角形,且
的長度為三邊長的三角形是直角三角形,且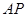 是斜邊.
是斜邊.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com