
【題目】對于實數a,我們規定:用符號![]() 表示不大于
表示不大于![]() 的最大整數,稱
的最大整數,稱![]() 為a的根整數,例如:
為a的根整數,例如: ![]() ,
, ![]() .
.
(1)仿照以上方法計算: ![]() = ;
= ; ![]() = .
= .
(2)若![]() =1,寫出滿足題意的x的整數值 .
=1,寫出滿足題意的x的整數值 .
如果我們對a連續求根整數,直到結果為1為止.例如:對10連續求根整數2次 ![]() ,這時候結果為1.
,這時候結果為1.
(3)對100連續求根整數, 次之后結果為1.
(4)只需進行3次連續求根整數運算后結果為1的所有正整數中,最大的是 .
【答案】(1) 2,5;(2) 1,2,3;(3)3;(4)255.
【解析】試題分析:
(1)由![]() ,
, ![]() 結合根整數的定義即可得到結果;
結合根整數的定義即可得到結果;
(2)由![]() 結合
結合![]() 可得x=1或2或3;
可得x=1或2或3;
(3)按題意對100連續求根整數至到結果為1即可得到所求答案;
(4)由![]() 結合22=4,42=16,162=256可知256是所有正整數中需連續進行4次求根整數的運算才能使結果為1的正整數中最小的一個,由此可知255是所有正整數中需連續經過3次求根整數運算才能使結果為1的正整數中最大的1個.
結合22=4,42=16,162=256可知256是所有正整數中需連續進行4次求根整數的運算才能使結果為1的正整數中最小的一個,由此可知255是所有正整數中需連續經過3次求根整數運算才能使結果為1的正整數中最大的1個.
試題解析:
(1)∵22=4,52=25,62=36,
∴5<![]() <6,
<6,
∴![]() =[2]=2,[
=[2]=2,[![]() ]=5,
]=5,
故答案為:2,5;
(2)∵12=1,22=4,且![]() ,
,
∴x=1,2,3,
故答案為:1,2,3;
(3)第一次:[![]() ]=10,
]=10,
第二次:[![]() ]=3,
]=3,
第三次:[![]() ]=1,
]=1,
故答案為:3;
(4)最大的正整數是255,理由如下:
∵[![]() ]=15,[
]=15,[![]() ]=3,[
]=3,[![]() ]=1,
]=1,
∴對255只需進行3次操作后變為1,
∵[![]() ]=16,[
]=16,[![]() ]=4,[
]=4,[![]() ]=2,[
]=2,[![]() ]=1,
]=1,
∴對256需進行4次操作后才能變為1,
∴只需進行3次操作后變為1的所有正整數中,最大的是255,
故答案為:255.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
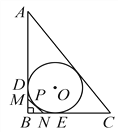
【題目】如圖,Rt△ABC的內切圓⊙O與兩直角邊AB、BC分別相切于點D、E,過劣弧![]() (不包括端點D、E)上任一點作⊙O的切線MN與AB、BC分別交于點M、N.若AC=10,BC=6,則△MBN的周長為__.
(不包括端點D、E)上任一點作⊙O的切線MN與AB、BC分別交于點M、N.若AC=10,BC=6,則△MBN的周長為__.
查看答案和解析>>
科目:初中數學 來源: 題型:
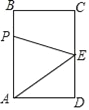
【題目】如圖,長方形ABCD中,AB=4cm,BC=3cm,E為CD的中點.動點P從A點出發,以每秒1cm的速度沿A﹣B﹣C﹣E運動,最終到達點E.若點P運動的時間為x秒,則當x=__時,△APE的面積等于5.
查看答案和解析>>
科目:初中數學 來源: 題型:
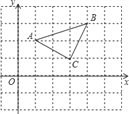
【題目】如圖所示,三角形ABC三個頂點A,B,C的坐標分別為A(1,2),B(4,3),C(3,1).
(1)三角形A1B1C1向右平移4個單位長度,再向下平移3個單位長度,恰好得到三角形ABC,試寫出三角形A1B1C1三個頂點的坐標.
(2)求△ABC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】金庸先生筆下的“五岳劍派”就是在以下五大名山中:
山名 | “東岳泰山” | “西岳華山” | “南岳衡山” | “北岳恒山” | “中岳嵩山” |
海拔(米) | 1545 | 2155 | 1300 | 2016 | 1491 |
若想根據表中數據繪制統計圖,以便更清楚的比較這五座山的高度,最合適的是( )
A.扇形統計圖B.折線統計圖C.條形統計圖D.以上都可以
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本題8分)如圖某幢大樓頂部有廣告牌CD.張老師目高MA為1.60米,他站立在離大樓45米的A處測得大樓頂端點D的仰角為30°;接著他向大樓前進14米、站在點B處,測得廣告牌頂端點C的仰角為45°.(取![]() ,計算結果保留一位小數)
,計算結果保留一位小數)

(1)求這幢大樓的高DH;
(2)求這塊廣告牌CD的高度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知![]() 中,
中, ![]() ,
, ![]() .如圖,將
.如圖,將![]() 進行折疊,使點
進行折疊,使點![]() 落在線段
落在線段![]() 上(包括點
上(包括點![]() 和點
和點![]() ),設點
),設點![]() 的落點為
的落點為![]() ,折痕為
,折痕為![]() ,當
,當![]() 是等腰三角形時,點
是等腰三角形時,點![]() 可能的位置共有( ).
可能的位置共有( ).

A. ![]() 種 B.
種 B. ![]() 種 C.
種 C. ![]() 種 D.
種 D. ![]() 種
種
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com