
【題目】如圖,![]() 為線段
為線段![]() 上一動點(不與點
上一動點(不與點![]() 、
、![]() 重合),在
重合),在![]() 同側分別作等邊
同側分別作等邊![]() 和等邊
和等邊![]() ,
,![]() 與
與![]() 交于點
交于點![]() ,
,![]() 與
與![]() 交于點
交于點![]() ,
,![]() 與
與![]() 交于點
交于點![]() ,連接
,連接![]() 、
、![]() ,以下五個結論:①
,以下五個結論:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() 平分
平分![]() .一定成立的結論有______________;
.一定成立的結論有______________;
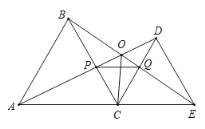
【答案】①②③⑤.
【解析】
①由于△ABC和△CDE是等邊三角形,可知AC=BC,CD=CE,∠ACB=∠DCE=60°,從而證出△ACD≌△BCE,可推知AD=BE;
②由△ACD≌△BCE得∠CBE=∠DAC,加之∠ACB=∠DCE=60°,AC=BC,得到△CQB≌△CPA(ASA),再根據∠PCQ=60°推出△PCQ為等邊三角形,又由∠PQC=∠DCE,根據內錯角相等,兩直線平行,可知②正確;
③根據②△CQB≌△CPA(ASA),可知③正確;
④根據∠DQE=∠ECQ+∠CEQ=60°+∠CEQ,∠CDE=60°,可知∠DQE≠∠CDE,可知④錯誤;
⑤由BC∥DE,得到∠CBE=∠BED,由∠CBE=∠DAE,得到∠AOB=∠OAE+∠AEO=60°可得出∠AOE=120°,再利用三角形相似以及等邊三角形的知識可知⑤正確;
解:∵等邊△ABC和等邊△CDE,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠BCD=∠DCE+∠BCD,即∠ACD=∠BCE,
在△ACD與△BCE中,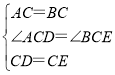 ,
,
∴△ACD≌△BCE(SAS),
∴AD=BE,
∴①正確;
∵△ACD≌△BCE,
∴∠CBE=∠DAC,
又∵∠ACB=∠DCE=60°,
∴∠BCD=60°,即∠ACP=∠BCQ,
又∵AC=BC,
∴△CQB≌△CPA(ASA),
∴CP=CQ,
又∵∠PCQ=60°可知△PCQ為等邊三角形,
∴∠PQC=∠DCE=60°,
∴PQ∥AE
∴②正確;
∵△CQB≌△CPA,
∴AP=BQ
∴③正確;
∵AD=BE,AP=BQ,
∴AD-AP=BE-BQ,
即DP=QE,
∵∠DQE=∠ECQ+∠CEQ=60°+∠CEQ,∠CDE=60°,
∴∠DQE≠∠CDE,故④錯誤;
∵BC∥DE,
∴∠CBE=∠BED,
∵∠CBE=∠DAE,
∴∠AOB=∠OAE+∠AEO=60°,
∴∠AOE=120°,
∵∠PBO=∠PAC,∠BOP=∠PCA,
∴△BPO∽△APC,
∴![]() ,
,
∴![]() ,
,
∵∠APB=∠CPO,
∴△APB∽△CPO,
∴∠COP=∠ABP=60°,
∴∠COA=∠COE=60°,
∴OC平分∠AOE,故⑤正確;
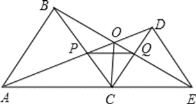
故答案為:①②③⑤.


 陽光課堂課時優化作業系列答案
陽光課堂課時優化作業系列答案科目:初中數學 來源: 題型:
【題目】如圖,某人為了測量小山頂上的塔ED的高,他在山下的點A處測得塔尖點D的仰角為45°,再沿AC方向前進60 m到達山腳點B,測得塔尖點D的仰角為60°,塔底點E的仰角為30°,求塔ED的高度.(結果保留根號)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀理解:
定義:有三個內角相等的四邊形叫“和諧四邊形”.
(1)在“和諧四邊形”![]() 中,若
中,若![]() ,則
,則![]() ;
;
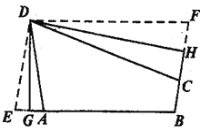
(2)如圖,折疊平行四邊形紙片![]() ,使頂點
,使頂點![]() ,
,![]() 分別落在邊
分別落在邊![]() ,
,![]() 上的點
上的點![]() ,
,![]() 處,折痕分別為
處,折痕分別為![]() ,
,![]() .
.
求證:四邊形![]() 是“和諧四邊形”.
是“和諧四邊形”.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠AOB=90°,射線OM平分∠AOC,ON平分∠BOC.

(1)如果∠BOC=30°,求∠MON的度數;
(2)如果∠AOB=α,∠BOC=30°,其他條件不變,求∠MON的度數;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將![]() 沿著過
沿著過![]() 中點
中點![]() 的直線折疊,使點
的直線折疊,使點![]() 落在
落在![]() 邊上的
邊上的![]() ,稱為第
,稱為第![]() 次操作,折痕
次操作,折痕![]() 到
到![]() 的距離記為
的距離記為![]() ;還原紙片后,再將
;還原紙片后,再將![]() 沿著過
沿著過![]() 中點
中點![]() 的直線折疊,使點
的直線折疊,使點![]() 落在
落在![]() 邊上的
邊上的![]() 處,稱為第
處,稱為第![]() 次操作,折痕
次操作,折痕![]() 到
到![]() 的距離記為
的距離記為![]() ;按上述方法不斷操作下去…,經過第
;按上述方法不斷操作下去…,經過第![]() 次操作后得到的折痕
次操作后得到的折痕![]() ,到
,到![]() 的距離記為
的距離記為![]() ,若
,若![]() ,則
,則![]() 的值為( )
的值為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,滑動調節式遮陽傘的立柱![]() 垂直于地面
垂直于地面![]() ,
,![]() 為立柱上的滑動調節點,傘體的截面示意圖為
為立柱上的滑動調節點,傘體的截面示意圖為![]() ,
,![]() 為
為![]() 中點,
中點,![]() ,
,![]() ,
,![]() ,
,![]() .當點
.當點![]() 位于初始位置
位于初始位置![]() 時,點
時,點![]() 與
與![]() 重合(圖2).根據生活經驗,當太陽光線與
重合(圖2).根據生活經驗,當太陽光線與![]() 垂直時,遮陽效果最佳.
垂直時,遮陽效果最佳.
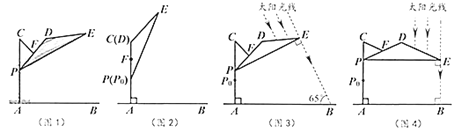
(1)上午10:00時,太陽光線與地面的夾角為![]() (圖3),為使遮陽效果最佳,點
(圖3),為使遮陽效果最佳,點![]() 需從
需從![]() 上調多少距離?(結果精確到
上調多少距離?(結果精確到![]() )
)
(2)中午12:00時,太陽光線與地面垂直(圖4),為使遮陽效果最佳,點![]() 在(1)的基礎上還需上調多少距離?(結果精確到
在(1)的基礎上還需上調多少距離?(結果精確到![]() )
)
(參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:在數軸上點![]() 表示數
表示數![]() ,點
,點![]() 表示數
表示數![]() ,點
,點![]() 表示數
表示數![]() ,
,![]() 是多項式
是多項式![]() 的一次項系數,
的一次項系數,![]() 是絕對值最小的整數,單項式
是絕對值最小的整數,單項式![]() 的次數為
的次數為![]() .
.
![]()
(1)![]() = ,
= ,![]() = ,
= ,![]() = ;
= ;
(2)若將數軸在點![]() 處折疊,則點
處折疊,則點![]() 與點
與點![]() 重合( 填“能”或“不能”);
重合( 填“能”或“不能”);
(3)點![]() 開始在數軸上運動,若點
開始在數軸上運動,若點![]() 以每秒1個單位長度的速度向右運動,同時,點
以每秒1個單位長度的速度向右運動,同時,點![]() 和點
和點![]() 分別以每秒3個單位長度和2個單位長度的速度向左運動,
分別以每秒3個單位長度和2個單位長度的速度向左運動,![]() 秒鐘過后,若點
秒鐘過后,若點![]() 與點B之間的距離表示為
與點B之間的距離表示為![]() ,點
,點![]() 與點
與點![]() 之間的距離表示為
之間的距離表示為![]() ,則
,則![]() = ,
= , ![]() = (用含
= (用含![]() 的代數式表示);
的代數式表示);
(4)請問:AB+BC的值是否隨著時間![]() 的變化而改變?若變化,請說明理由;若不變,請求其值.
的變化而改變?若變化,請說明理由;若不變,請求其值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】直線AB與直線CD相交于點O,OE平分![]() .
.
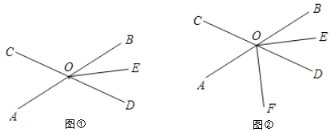
(1)如圖①,若![]() ,求
,求![]() 的度數;
的度數;
(2)如圖②,射線OF在![]() 內部.
內部.
①若![]() ,判斷OF是否為
,判斷OF是否為![]() 的平分線,并說明理由;
的平分線,并說明理由;
②若OF平分![]() ,
,![]() ,求
,求![]() 的度數.
的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是二次函數y=ax2+bx+c(a,b,c是常數,a≠0)圖象的一部分,與x軸的交點A在點(2,0)和(3,0)之間,對稱軸是x=1.對于下列說法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m為實數);⑤當﹣1<x<3時,y>0,其中正確的是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com