
如圖,
PA、PB是⊙O的切線,A、B為切點(diǎn),∠OAB=30°.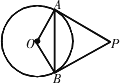
(1)求∠APB的度數(shù);
(2)當(dāng)OA=3時(shí),求AP的長(zhǎng).
|
分析: (1)可以在四邊形OAPB中利用“四邊形的內(nèi)角和等于360°”求解,也可以在△ABP中求解,主要是利用切線的性質(zhì)和切線長(zhǎng)定理;(2)連接OP或過點(diǎn)O作OD⊥AB,構(gòu)造直角三角形來(lái)求解.解: (1)方法一:在△ ABO中,因?yàn)?/FONT>OA=OB,∠OAB=30°,所以∠AOB=180°-2×30°=120°.因?yàn)?/FONT> PA、PB是⊙O的切線,所以OA⊥PA,OB⊥PB,即∠OAP=∠OBP=90°.所以在四邊形 OAPB中,∠APB=360°-120°-90°-90°=60°.方法二:因?yàn)?/FONT> PA、PB是⊙O的切線,所以PA=PB,OA⊥PA.因?yàn)椤?/FONT> OAB=30°,所以∠BAP=∠OAP-∠OAB=90°-30°=60°.所以△ ABP是等邊三角形.所以∠ APB=60°.(2)方法一:如圖,連接OP.
因?yàn)?/FONT> PA、PB是⊙O的切線,所以PO平分∠APB,即∠APO=在 Rt△OAP中,OA=3,∠APO=30°,所以AP=3方法二:如圖,過點(diǎn) O作OD⊥AB于點(diǎn)D.
因?yàn)樵凇?/FONT> OAB中,OA=OB,所以AD=在 Rt△AOD中,OA=3,∠OAD=30°,所以AD=OAcos30°=3×由 (1)知,△APB是等邊三角形,所以AP=AB=2AD=3點(diǎn)評(píng):圓的切線的性質(zhì)不僅表現(xiàn)在圓的切線長(zhǎng)定理的兩個(gè)結(jié)論上,而且表現(xiàn)在它與等腰三角形、垂徑定理、相似三角形等知識(shí)相聯(lián)系而形成的基本圖形所得出的許多重要性質(zhì). |



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
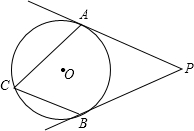 如圖,PA,PB是⊙O的切線,切點(diǎn)分別為A,B,且∠APB=50°,點(diǎn)C是優(yōu)弧
如圖,PA,PB是⊙O的切線,切點(diǎn)分別為A,B,且∠APB=50°,點(diǎn)C是優(yōu)弧 | AB |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
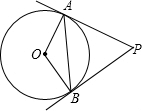 如圖,PA、PB是⊙O的切線,A、B為切點(diǎn),∠OAB=30度.
如圖,PA、PB是⊙O的切線,A、B為切點(diǎn),∠OAB=30度.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
 4、如圖,PA、PB是⊙O的兩條切線,A、B是切點(diǎn),連接AB,直線PO交AB于M.請(qǐng)你根據(jù)圓的對(duì)稱性,寫出△PAB的三個(gè)正確的結(jié)論.
4、如圖,PA、PB是⊙O的兩條切線,A、B是切點(diǎn),連接AB,直線PO交AB于M.請(qǐng)你根據(jù)圓的對(duì)稱性,寫出△PAB的三個(gè)正確的結(jié)論.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
 (2012•谷城縣模擬)如圖,PA、PB是⊙O 的切線,切點(diǎn)分別是A、B,點(diǎn)C是⊙O上異與點(diǎn)A、B的點(diǎn),如果∠P=60°,那么∠ACB等于
(2012•谷城縣模擬)如圖,PA、PB是⊙O 的切線,切點(diǎn)分別是A、B,點(diǎn)C是⊙O上異與點(diǎn)A、B的點(diǎn),如果∠P=60°,那么∠ACB等于查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com