
 如圖,以△ABC的一邊AB為直徑作⊙O,⊙O與BC邊的交點D恰好為BC的中點,過點D作⊙O的切線交AC邊于點E.
如圖,以△ABC的一邊AB為直徑作⊙O,⊙O與BC邊的交點D恰好為BC的中點,過點D作⊙O的切線交AC邊于點E. ,求
,求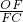 的值.
的值. (1)證明:連接OD.
(1)證明:連接OD.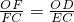 .
. =
= ,
,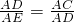 .
.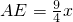 .
.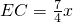 .
.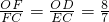 .
. =
= ,故設AD=3x,則AB=AC=4x,OD=2x;由相似三角形△ADC∽△AED的對應邊成比例得到AD2=AE•AC.則
,故設AD=3x,則AB=AC=4x,OD=2x;由相似三角形△ADC∽△AED的對應邊成比例得到AD2=AE•AC.則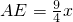 ,
,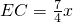 ,所以
,所以 .
.

科目:初中數學 來源: 題型:
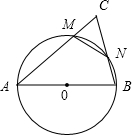 如圖,以△ABC的邊AB為直徑畫圓,與邊AC交于M,與邊BC交于N,已知△ABC的面積是△CMN面積的4倍,△ABC中有一個內角度數是另一內角度數的2倍,試計算△ABC三個內角的度數:
如圖,以△ABC的邊AB為直徑畫圓,與邊AC交于M,與邊BC交于N,已知△ABC的面積是△CMN面積的4倍,△ABC中有一個內角度數是另一內角度數的2倍,試計算△ABC三個內角的度數:查看答案和解析>>
科目:初中數學 來源: 題型:
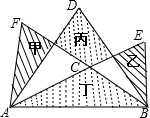 如圖,以△ABC的每一條邊為邊作三個正三角形△ABD、△BCE和△ACF.已知這三個正三角形構成的圖形中,甲、乙陰影部分的面積和等于丙、丁陰影部分的面積和,則∠FCE=( )
如圖,以△ABC的每一條邊為邊作三個正三角形△ABD、△BCE和△ACF.已知這三個正三角形構成的圖形中,甲、乙陰影部分的面積和等于丙、丁陰影部分的面積和,則∠FCE=( )| A、130° | B、140° | C、150° | D、160° |
查看答案和解析>>
科目:初中數學 來源: 題型:
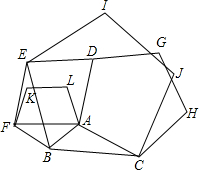 (2012•拱墅區一模)如圖,以△ABC的各邊為邊,在BC的同側分別作三個正五邊形.它們分別是正五邊形ABFKL、BCJIE、ACHGD,試探究:
(2012•拱墅區一模)如圖,以△ABC的各邊為邊,在BC的同側分別作三個正五邊形.它們分別是正五邊形ABFKL、BCJIE、ACHGD,試探究:查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com