
【題目】下表中,y是x的一次函數.
x |
| 1 | 2 | 5 | |
y | 6 |
|
|
|
(1)求該函數的表達式,并補全表格;
(2)已知該函數圖象上一點M(1,-3)也在反比例函數![]() 圖象上,求這兩個函數圖象的另一交點N的坐標.
圖象上,求這兩個函數圖象的另一交點N的坐標.
【答案】(1)y=-3x,補全表格見解析;(2)(-1,3).
【解析】
試題(1)設y=kx+b,將任已知兩點代入可得函數解析式,從而補全表格.
(2)將點M的坐標代入![]() ,可得m的值,聯立一次函數及反比例函數解析式可得另一交點坐標.
,可得m的值,聯立一次函數及反比例函數解析式可得另一交點坐標.
試題解析:解:(1)設該一次函數為y=kx+b(k≠0),
∵當x=-2時,y=6,當x=1時,y=-3,
∴![]() ,解得:
,解得:![]() .
.
∴一次函數的表達式為:y=-3x.
∵當x=2時,y=-6;當y=-12時,x=4,
補全表格如下:
x |
| 1 | 2 | 4 | 5 |
y | 6 |
| -6 |
|
|
(2)∵點M(1,-3)在反比例函數![]() 上(m≠0),
上(m≠0),
∴![]() ,解得m=-3到.
,解得m=-3到.
∴反比例函數解析式為![]() .
.
聯立可得 ,解得:
,解得:![]() 或
或![]() .
.
∴另一交點坐標為(-1,3).


 小學教材全測系列答案
小學教材全測系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知![]() 與
與![]() 均是等邊三角形,點
均是等邊三角形,點![]() 在同一條直線上,
在同一條直線上,![]() 與
與![]() 交于點
交于點![]() ,
,![]() 與
與![]() 交于點
交于點![]() ,
,![]() 與
與![]() 交于點
交于點![]() ,連接
,連接![]() ,則下列結論:①
,則下列結論:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中正確的個數是( )
,其中正確的個數是( )
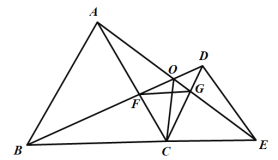
A.1B.2C.3D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①ABCD的對角線AC和BD相交于點O,EF過點O且與邊AB,CD分別相交于點E和點F.
(1)求證:OE=OF
(2)如圖②,已知AD=1,BD=2,AC=2![]() ,∠DOF=∠α,
,∠DOF=∠α,
①當∠α為多少度時,EF⊥AC?
②連結AF,求△ADF的周長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,D是BC邊的中點,分別過B、C做射線AD的垂線,垂足分別為E、F,連接BF、CE.
(1)求證:四邊形BECF是平行四邊形;
(2)我們知道S△ABD=S△ACD,若AF=FD,在不添加輔助線的條件下,直接寫出與△ABD、△ACD面積相等的所有三角形.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我國古代數學家趙爽“的勾股圓方圖”是由四個全等的直角三角形與中間的一個小正方形拼成的一個大正方形(如圖所示),如果大正方形的面積是25,小正方形的面積是1,直角三角形的兩直角邊分別是a、b,那么![]() 的值為( ).
的值為( ).

A. 49 B. 25 C. 13 D. 1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,矩形的一條邊長為x,周長的一半為y,定義(x,y)為這個矩形的坐標。如圖2,在平面直角坐標系中,直線x=1,y=3將第一象限劃分成4個區域,已知矩形1的坐標的對應點A落在如圖所示的雙曲線上,矩形2的坐標的對應點落在區域④中,則下面敘述中正確的是( )

A. 點A的橫坐標有可能大于3
B. 矩形1是正方形時,點A位于區域②
C. 當點A沿雙曲線向上移動時,矩形1的面積減小
D. 當點A位于區域①時,矩形1可能和矩形2全等
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,四邊形ABOC是正方形,點A的坐標為(1,1),![]() 是以點B為圓心,BA為半徑的圓弧;
是以點B為圓心,BA為半徑的圓弧;![]() 是以點O為圓心,OA1為半徑的圓弧;
是以點O為圓心,OA1為半徑的圓弧;![]() 是以點C為圓心,CA2為半徑的圓弧;
是以點C為圓心,CA2為半徑的圓弧;![]() 是以點A為圓心,AA3為半徑的圓弧,它們所對的圓心角都等于90°。繼續以點B、O、C、A為圓心按上述做法得到的曲線AA1A2A3A4A5……稱為“正方形的漸開線”,那么點A5的坐標是________,點A2018的坐標是_________
是以點A為圓心,AA3為半徑的圓弧,它們所對的圓心角都等于90°。繼續以點B、O、C、A為圓心按上述做法得到的曲線AA1A2A3A4A5……稱為“正方形的漸開線”,那么點A5的坐標是________,點A2018的坐標是_________

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某“數學興趣小組”根據學習函數的經驗,對函數![]() 的圖象和性質進行了探究,探究過程如下,請補充完整:
的圖象和性質進行了探究,探究過程如下,請補充完整:
(1)自變量x的取值范圍是全體實數,x與y的幾組對應數值如下表:
x | … | -3 | - | -2 | -1 | 0 | 1 | 2 |
| 3 | … |
y | … | -2 | - | m | 2 | 1 | 2 | 1 | - | -2 | … |
其中m=____________;
(2)如圖,在平面直角坐標系xOy中,描出了以上表中各對對應值為坐標的點,根據描出的點,畫出該函數的圖象;

(3)根據函數圖象
①寫出該函數的一條性質_______________;
②直線![]() 經過點(-l,2),若關于x的方程
經過點(-l,2),若關于x的方程![]() 有4個互不相等的實數根,則b的取值范圍是__________________.
有4個互不相等的實數根,則b的取值范圍是__________________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在![]() 中,
中,![]() ,
,![]() ,直線
,直線![]() 經過點
經過點![]() ,且
,且![]() 于點
于點![]() ,
,![]() 于點
于點![]() .
.

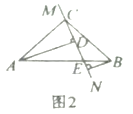
(1)當直線![]() 繞點
繞點![]() 旋轉到圖1的位置時,求證:
旋轉到圖1的位置時,求證:
①![]() ;
;
②![]() .
.
(2)當直線![]() 繞點
繞點![]() 旋轉到圖2的位置時,第(1)問中的兩個結論是否還成立,請說明理由.
旋轉到圖2的位置時,第(1)問中的兩個結論是否還成立,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com