
【題目】如圖,等邊△AOB中點O是原點,點A在y軸上,點B的坐標是(2 ![]() ,2),小明做一個數學實驗,在x軸上取一動點C,以AC為一邊畫出等邊△ACP,移動點C時,探究點P的位置變化情況.
,2),小明做一個數學實驗,在x軸上取一動點C,以AC為一邊畫出等邊△ACP,移動點C時,探究點P的位置變化情況.
(1)如圖,小明將點C移至x軸負半軸,在AC的右側畫出等邊△ACP,并使得頂點P在第三象限時,連接BP,求證:△AOC≌△ABP;
(2)小明在x軸上移動點C,并在AC的右側畫出等邊△ACP時,發現點P在某函數圖象上,請求出點P所在函數圖象的解析式.
(3)小明在x軸上移動點C點時,若在AC的左側畫出等邊△ACP,點P會不會在某函數圖象上?若會在某函數圖象上,請直接寫出該函數圖象的解析式,若不在某函數圖象上,請說明理由.
【答案】
(1)
證明:如圖,
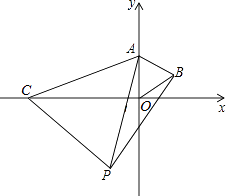
∵△AOB與△ACP都是等邊三角形,
∴OA=AB,A=AP,CAP=∠OAB=60°.
∴∠CAP+∠PAO=∠OAB+∠PAO.
∴∠CAO=∠PAB.
在△AOC與△PAB中,
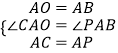 ,
,
∴△AOC≌△ABP
(2)
解:由(1)可知,△AOC≌△ABP,
∴∠COA=∠PBA=90°,
∴點P在過點A且與AB垂直的直線上,
在等邊△AOB中,B(2 ![]() ,2),
,2),
∴AB=4,
當點C移動,使得P在y軸上時,
∵△PAB是直角三角形,∠PAB=60°,
∴PA= ![]() =8,
=8,
∴P(0,﹣4),
設直線PB的解析式為y=kx﹣4,把B(2 ![]() ,2)代入得到k=
,2)代入得到k= ![]() ,
,
∴點P所在函數圖象的解析式為y= ![]() x﹣4
x﹣4
(3)
會在函數的圖象上,如圖作B的對稱點B′,連接AB′,OB′.
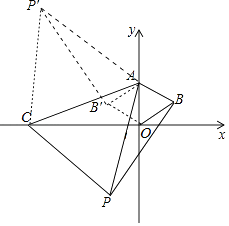
由(2)可知,P′B′⊥AB′,同法可得直線P′B′的解析式為t=﹣ ![]() x﹣4.
x﹣4.
∴該函數圖象的解析式為y=﹣ ![]() x﹣4
x﹣4
【解析】(1)利用等邊三角形的性質,根據SAS根據解決問題.(2)首先證明點P在過點A且與AB垂直的直線上,求出特殊點(P在y軸上的點),利用待定系數法即可解決問題.(3)如圖作B的對稱點B′,連接AB′,OB′.由(2)可知,P′B′⊥AB′,同法可得直線P′B′的解析式為t=﹣ ![]() x﹣4.
x﹣4.
【考點精析】通過靈活運用等邊三角形的性質,掌握等邊三角形的三個角都相等并且每個角都是60°即可以解答此題.


 快樂暑假暑假能力自測中西書局系列答案
快樂暑假暑假能力自測中西書局系列答案科目:初中數學 來源: 題型:
【題目】![]() 如圖
如圖![]() 所示,在
所示,在![]() 中,
中,![]() 的垂直平分線交
的垂直平分線交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() .
.![]() 的垂直平分線交
的垂直平分線交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() ,連接
,連接![]() 、
、![]() ,求證:
,求證:![]() 的周長
的周長![]() ;21.
;21.
![]() 如圖
如圖![]() 所示,在
所示,在![]() 中,若
中,若![]() ,
,![]() ,
,![]() 的垂直平分線交
的垂直平分線交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() .
.![]() 的垂直平分線交
的垂直平分線交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() ,連接
,連接![]() 、
、![]() ,試判斷
,試判斷![]() 的形狀,并證明你的結論.
的形狀,并證明你的結論.
![]() 如圖
如圖![]() 所示,在
所示,在![]() 中,若
中,若![]() ,
,![]() 的垂直平分線交
的垂直平分線交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() ,
,![]() 的垂直平分線交
的垂直平分線交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() ,連接
,連接![]() 、
、![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的長.
的長.


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,A(﹣2,0),C(2,2),過C作CB⊥x軸于B.

(1)如圖1,△ABC的面積是 ;
(2)如圖1,在y軸上找一點P,使得△ABP的面積與△ABC的面積相等,請直接寫出P點坐標: ;
(3)如圖2,若過B作BD∥AC交y軸于D,則∠BAC+∠ODB的度數為 度;
(4)如圖3,BD∥AC,若AE、DE分別平分∠CAB,∠ODB,求∠AED的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在直角坐標系中,已知點![]() ,
,![]() ,
,![]() ,a是
,a是![]() 的立方根,方程
的立方根,方程![]() 是關于x,y的二元一次方程,d為不等式組
是關于x,y的二元一次方程,d為不等式組![]() 的最大整數解.
的最大整數解.
![]() 求點A、B、C的坐標;
求點A、B、C的坐標;
![]() 如圖1,若D為y軸負半軸上的一個動點,當
如圖1,若D為y軸負半軸上的一個動點,當![]() 時,
時,![]() 與
與![]() 的平分線交于M點,求
的平分線交于M點,求![]() 的度數;
的度數;
![]() 如圖2,若D為y軸負半軸上的一個動點,連BD交x軸于點E,問是否存在點D,使
如圖2,若D為y軸負半軸上的一個動點,連BD交x軸于點E,問是否存在點D,使![]() ?若存在,請求出D的縱坐標
?若存在,請求出D的縱坐標![]() 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,規定把一個點先繞原點逆時針旋轉45°,再作出它關于原點的對稱點稱為一次變換,已知點A的坐標為(﹣2,0),把點A經過連續2014次這樣的變換得到的點A2014的坐標是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,則下列結論:①a+b+c<0;②a﹣b+c<0;③b+2a<0;④abc>0,其中正確的是(填編號) 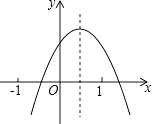
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:在平面直角坐標系中,網格中每一個小正方形的邊長為1個單位長度;已知△ABC. 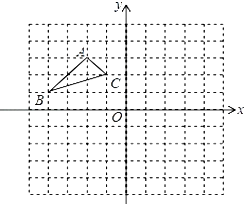
(1)作出△ABC關于x軸對稱的△A1B1C1 , (只畫出圖形).
(2)作出△ABC關于原點O成中心對稱的△A2B2C2 , (只畫出圖形),寫出B2和C2的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com