
【題目】(1)(閱讀與證明)
如圖1,在正![]() 的外角
的外角![]() 內引射線
內引射線![]() ,作點C關于
,作點C關于![]() 的對稱點E(點E在
的對稱點E(點E在![]() 內),連接
內),連接![]() ,
,![]() 、
、![]() 分別交
分別交![]() 于點F、G.
于點F、G.
①完成證明:![]() 點E是點C關于
點E是點C關于![]() 的對稱點,
的對稱點,
![]() ,
,![]() ,
,![]() .
.
![]() 正
正![]() 中,
中,![]() ,
,![]() ,
,
![]() ,得
,得![]() .
.
在![]() 中,
中,![]() ,
,![]() ______
______![]() .
.
在![]() 中,
中,![]() ,
,![]() ______
______![]() .
.
②求證:![]() .
.
(2)(類比與探究)
把(1)中的“正![]() ”改為“正方形
”改為“正方形![]() ”,其余條件不變,如圖2.類比探究,可得:
”,其余條件不變,如圖2.類比探究,可得:
①![]() ______
______![]() ;
;
②線段![]() 、
、![]() 、
、![]() 之間存在數量關系___________.
之間存在數量關系___________.
(3)(歸納與拓展)
如圖3,點A在射線![]() 上,
上,![]() ,
,![]() ,在
,在![]() 內引射線
內引射線![]() ,作點C關于
,作點C關于![]() 的對稱點E(點E在
的對稱點E(點E在![]() 內),連接
內),連接![]() ,
,![]() 、
、![]() 分別交
分別交![]() 于點F、G.則線段
于點F、G.則線段![]() 、
、![]() 、
、![]() 之間的數量關系為__________.
之間的數量關系為__________.
【答案】(1)①60°,30°;②證明見解析;(2)①45°;②BF=![]() (AF+FG);(3)
(AF+FG);(3)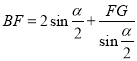 .
.
【解析】
(1)①根據等量代換和直角三角形的性質即可確定答案;②在FB上取AN=AF,連接AN.先證明△AFN是等邊三角形,得到 ∠BAN=∠2=∠1,然后再證明△ABN≌△AEF,然后利用全等三角形的性質以及線段的和差即可證明;
(2)類比(1)的方法即可作答;
(3)根據(1)(2)的結論,即可總結出答案.
解:(1)①∵![]() ,
,![]() ,
,![]()
∴![]() ,即
,即![]() 60°;
60°;
∵![]()
∴![]()
故答案為60°,30°;
②在FB上取FN=AF,連接AN
∵∠AFN=∠EFG=60°
∴△AFN是等邊三角形
∴AF=FN=AN
∵FN=AF
∴∠BAC=∠NAF=60°
∴∠BAN+∠NAC=∠NAC+∠2
∴∠BAN=∠2
∵點C關于![]() 的對稱點E
的對稱點E
∴∠2=∠1,AC=AE
∴∠BAN=∠2=∠1
∵AB=AC
∴AB=AE
在△ABN和△AEF
FN=AF,∠BAN=∠1,AB=AE
∴△ABN≌△AEF
∴BN=EF
∵AG⊥CE,∠FEG=30°
∴EF=2FG
∴BN=EF=2FG
∵BF=BN+NF
∴BF=2FG+AF
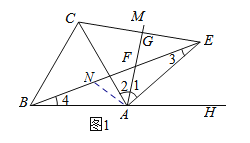
(2)①![]() 點E是點C關于
點E是點C關于![]() 的對稱點,
的對稱點,
![]() ,
,![]() ,
,![]() .
.
![]() 正方形ABCD中,
正方形ABCD中,![]() ,
,![]() ,
,
![]() ,得
,得![]() .
.
在![]() 中,
中,![]() ,
,
![]() 45
45![]() .
.
在![]() 中,
中,![]() ,
,
![]() 45
45![]() .
.
故答案為45°;
②在FB上取FN=AF,連接AN
∵∠AFN=∠EFG=45°
∴△AFN是等腰直角三角形
∴∠NAF=90°,AF=AN
∴∠BAN+∠NAC=∠NAC+∠2=90°,FN=![]() AF
AF
∴∠BAN=∠2
∵點C關于![]() 的對稱點E
的對稱點E
∴∠2=∠1,AC=AE
∴∠BAN=∠2=∠1
∵AB=AC
∴AB=AE
在△ABN和△AEF
FN=AF,∠BAN=∠1,AB=AE
∴△ABN≌△AEF
∴BN=EF
∵AG⊥CE,∠FEG=45°
∴EF=![]() FG
FG
∴BN=EF=![]() FG
FG
∵BF=BN+NF
∴BF=![]() FG+
FG+![]() AF
AF
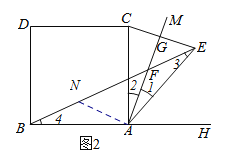
(3)由(1)得:當∠BAC=60°時
BF=AF+2FG=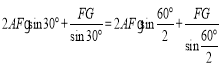
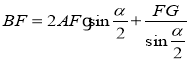 ;
;
由(2)得:當∠BAC=90°時
BF=![]() AF+
AF+![]() 2FG=
2FG=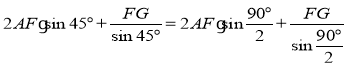 ;
;
以此類推,當當∠BAC=![]() 60°時,
60°時,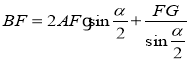 .
.


科目:初中數學 來源: 題型:
【題目】閱讀材料解答下列問題
觀察下列方程:①![]() ,②
,②![]() ,③
,③![]() ……
……
⑴按此規律寫出關于x的第n個方程為____________________,此方程的解為____________.
⑵根據上述結論,求出![]() 的解.
的解.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一勘測人員從山腳![]() 點出發,沿坡度為
點出發,沿坡度為![]() 的坡面
的坡面![]() 行至
行至![]() 點處時,他的垂直高度上升了
點處時,他的垂直高度上升了![]() 米;然后再從
米;然后再從![]() 點處沿坡角為
點處沿坡角為![]() 的坡面
的坡面![]() 以
以![]() 米/分鐘的速度到達山頂
米/分鐘的速度到達山頂![]() 點時,用了
點時,用了![]() 分鐘.
分鐘.
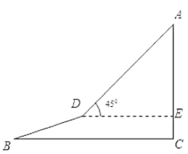
(1)求![]() 點到
點到![]() 點之間的水平距離;
點之間的水平距離;
(2)求山頂![]() 點處的垂直高度
點處的垂直高度![]() 是多少米?(
是多少米?(![]() 結果保留整數)
結果保留整數)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解學生掌握垃圾分類知識的情況,增強學生環保意識,某學校舉行了“垃圾分類人人有責”的知識測試活動,現從該校七、八年級中各隨機抽取20名學生的測試成績(滿分10分,6分及6分以上為合格)進行整理、描述和分析,下面給出了部分信息.
七年級20名學生的測試成績為:
7,8,7,9,7,6,5,9,10,9,8,5,8,7,6,7,9,7,10,6.
七、八年級抽取的學生的測試成績的平均數、眾數、中位數、8分及以上人數所占百分比如下表所示:
年級 | 平均數 | 眾數 | 中位數 | 8分及以上人數所占百分比 |
七年級 | 7.5 | a | 7 | 45% |
八年級 | 7.5 | 8 | b | c |
八年級20名學生的測試成績條形統計圖如圖:
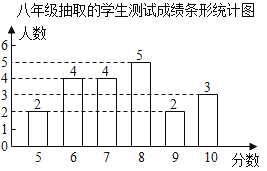
根據以上信息,解答下列問題:
(1)直接寫出上述表中的a,b,c的值;
(2)根據以上數據,你認為該校七、八年級中哪個年級學生掌握垃圾分類知識較好?請說明理由(寫出一條理由即可);
(3)該校七、八年級共1200名學生參加了此次測試活動,估計參加此次測試活動成績合格的學生人數是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
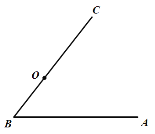
【題目】如圖,點O在![]() 的邊
的邊![]() 上,以
上,以![]() 為半徑作
為半徑作![]() ,
,![]() 的平分線
的平分線![]() 交
交![]() 于點D,過點D作
于點D,過點D作![]() 于點E.
于點E.
(1)尺規作圖(不寫作法,保留作圖痕跡),補全圖形;
(2)判斷![]() 與
與![]() 交點的個數,并說明理由.
交點的個數,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
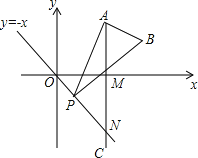
【題目】如圖,已知點A是第一象限內橫坐標為![]() 的一個定點,AC⊥x軸于點M,交直線y=﹣x于點N.若點P是線段ON上的一個動點,∠APB=30°,BA⊥PA,則點P在線段ON上運動時,A點不變,B點隨之運動.求當點P從點O運動到點N時,點B運動的路徑長是_____.
的一個定點,AC⊥x軸于點M,交直線y=﹣x于點N.若點P是線段ON上的一個動點,∠APB=30°,BA⊥PA,則點P在線段ON上運動時,A點不變,B點隨之運動.求當點P從點O運動到點N時,點B運動的路徑長是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了增強環境保護意識,在“世界環境日”當天,在環保局工作人員指導下,若干名“環保小衛士”組成的“控制噪聲污染”課題學習研究小組,隨機抽查了全市40個噪聲測量點在某時刻的噪聲聲級(單位:dB),并將抽查得到的數據進行整理(設所測數據是正整數),得頻數分布表如下:
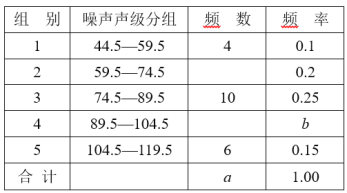

根據表中提供的信息解答下列問題:
(1)頻數分布表中的a= ,b= ;
(2)補充完整頻數分布直方圖;
(3)這組數據的中位數落在第 小組內;
(4)如果全市共有400個測量點,那么在這一時刻噪聲聲級小于75dB的測量點約有多少個?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為紀念“五四運動”100周年,某校舉行了征文比賽,該校學生全部參加了比賽.比賽設置一等、二等、三等三個獎項,賽后該校對學生獲獎情況做了抽樣調查,并將所得數據繪制成如圖所示的兩幅不完整的統計圖.根據圖中信息解答下列問題:
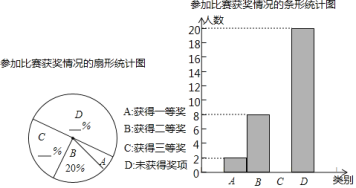
(1)本次抽樣調查學生的人數為 .
(2)補全兩個統計圖,并求出扇形統計圖中A所對應扇形圓心角的度數.
(3)若該校共有840名學生,請根據抽樣調查結果估計獲得三等獎的人數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com