
【題目】利用“同角的余角相等”可以幫助我們得到相等的角,這個規律在全等三角形的判定中有著廣泛的運用.
(1)如圖①,![]() ,
,![]() ,
,![]() 三點共線,
三點共線,![]() 于點
于點![]() ,
,![]() 于點
于點![]() ,
,![]() ,且
,且![]() .若
.若![]() ,求
,求![]() 的長.
的長.
(2)如圖②,在平面直角坐標系中,![]() 為等腰直角三角形,直角頂點
為等腰直角三角形,直角頂點![]() 的坐標為
的坐標為![]() ,點
,點![]() 的坐標為
的坐標為![]() .求直線
.求直線![]() 與
與![]() 軸的交點坐標.
軸的交點坐標.
(3)如圖③,![]() ,
,![]() 平分
平分![]() ,若點
,若點![]() 坐標為
坐標為![]() ,點
,點![]() 坐標為
坐標為![]() .則
.則![]() .(只需寫出結果,用含
.(只需寫出結果,用含![]() ,
,![]() 的式子表示)
的式子表示)

【答案】(1)6;(2)(0,2);(3)![]()
【解析】
(1)利用AAS證出△ABC≌△CDE,根據全等三角形的性質可得AB=CD,BC=DE,再根據BD=CD+BC等量代換即可求出BD;
(2)過點A作AD⊥x軸于D,過點B作BE⊥x軸于E,利用AAS證出△ADC≌△CEB,根據全等三角形的性質可得AD=CE,CD=BE,根據點A和點C的坐標即可求出點B的坐標,然后利用待定系數法求出直線AB的解析式,即可求出直線AB與y軸的交點坐標;
(3)過點C作CD⊥y軸于D,CE⊥x軸于E,根據正方形的判定可得四邊形OECD是正方形,然后利用ASA證出△DCA≌△ECB,從而得出DA=EB,S△DCA=S△ECB,然后利用正方形的邊長相等即可求出a、b表示出DA和正方形的邊長OD,然后根據![]() 即可推出
即可推出![]() =
=![]() ,最后求正方形的面積即可.
,最后求正方形的面積即可.
解:(1)∵![]() ,
,![]() ,
,![]()
∴∠ABC=∠CDE=∠ACE=90°
∴∠A+∠ACB=90°,∠ECD+∠ACB=180°-∠ACE=90°
∴∠A=∠ECD
在△ABC和△CDE中
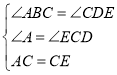
∴△ABC≌△CDE
∴AB=CD,BC=DE
∴BD=CD+BC=![]()
(2)過點A作AD⊥x軸于D,過點B作BE⊥x軸于E
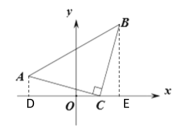
∵△ABC為等腰直角三角形
∴∠ADC=∠CEB=∠ACB=90°,AC=CB
∴∠DAC+∠ACD=90°,∠ECB+∠ACD=180°-∠ACB=90°
∴∠DAC =∠ECB
在△ADC和△CEB中
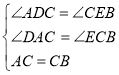
∴△ADC≌△CEB
∴AD=CE,CD=BE
∵點![]() 的坐標為
的坐標為![]() ,點
,點![]() 的坐標為
的坐標為![]()
∴CO=1,AD=1,DO=2,
∴OE=OC+CE= OC+AD=2,BE=CD=CO+DO=3,
∴點B的坐標為(2,3)
設直線AB的解析式為y=kx+b
將A、B兩點的坐標代入,得
![]()
解得:![]()
∴直線AB的解析式為![]()
當x=0時,解得y=2
∴直線![]() 與
與![]() 軸的交點坐標為(0,2);
軸的交點坐標為(0,2);
(3)過點C作CD⊥y軸于D,CE⊥x軸于E
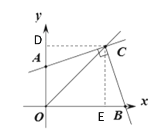
∵OC平分∠AOB
∴CD=CE
∴四邊形OECD是正方形
∴∠DCE=90°,OD=OE
∵∠ACB=90°
∴∠DCA+∠ACE=∠ECB+∠ACE=90°
∴∠DCA=∠ECB
在△DCA和△ECB中
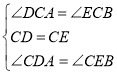
∴△DCA≌△ECB
∴DA=EB,S△DCA=S△ECB
∵點![]() 坐標為
坐標為![]() ,點
,點![]() 坐標為
坐標為![]()
∴OB=b,OA=a
∵OD=OE
∴OA+DA=OB-BE
即a+DA=b-DA
∴DA=![]()
∴OD= OA+DA=![]()
![]()
=![]()
=![]()
= DA2
=![]()
=![]()
故答案為:![]() .
.


科目:初中數學 來源: 題型:
【題目】已知,點B在線段CE上.
(感知)(1)如圖①,∠C=∠ABD=∠E=90°,易知△ACB∽△AED(不要求證明);
(拓展)(2)如圖②,△ACE中,AC=AE,且∠ABD=∠E,求證:△ACB∽△BED;
(應用)(3)如圖③,△ACE為等邊三角形,且∠ABD=60°,AC=6,BC=2,則△ABD與△BDE的面積比為 .
查看答案和解析>>
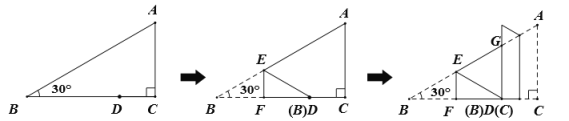
科目:初中數學 來源: 題型:
【題目】在三角形紙片![]() 中,
中,![]() ,
,![]() ,點
,點![]() (不與
(不與![]() ,
,![]() 重合)是
重合)是![]() 上任意一點,將此三角形紙片按下列方式折疊,若
上任意一點,將此三角形紙片按下列方式折疊,若![]() 的長度為
的長度為![]() ,則
,則![]() 的周長為__________.(用含
的周長為__________.(用含![]() 的式子表示)
的式子表示)
查看答案和解析>>
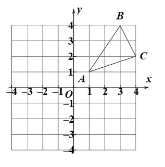
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,![]() 的三個頂點坐標分別為
的三個頂點坐標分別為![]() ,
,![]() ,
,![]() .
.
(1)在圖中畫出![]() 關于
關于![]() 軸對稱的
軸對稱的![]() ;
;
(2)通過平移,使![]() 移動到原點
移動到原點![]() 的位置,畫出平移后的
的位置,畫出平移后的![]() .
.
(3)在![]() 中有一點
中有一點![]() ,則經過以上兩次變換后點
,則經過以上兩次變換后點![]() 的對應點
的對應點![]() 的坐標為 .
的坐標為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD中,M為BC上一點,F是AM的中點,EF⊥AM,垂足為F,交AD的延長線于點E,交DC于點N.

(1)求證:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知有兩輛玩具車進行30米的直跑道比賽,兩車從起點同時出發,A車到達終點時,B車離終點還差12米,A車的平均速度為2.5米/秒.
(1)求B車的平均速度;
(2)如果兩車重新比賽,A車從起點退后12米,兩車能否同時到達終點?請說明理由;
(3)在(2)的條件下,若調整A車的平均速度,使兩車恰好同時到達終點,求調整后A車的平均速度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數學課上,李老師出示了如下的題目:如圖1,在等邊![]() 中,點
中,點![]() 在
在![]() 上,點
上,點![]() 在
在![]() 的延長線上,且
的延長線上,且![]() ,試確定線段
,試確定線段![]() 與
與![]() 的大小關系,并說明理由,
的大小關系,并說明理由,
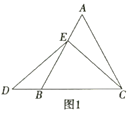
(1)小敏與同桌小聰探究解答的思路如下:
①特殊情況,探索結論,
當點![]() 為
為![]() 的中點時,如圖2,確定線段
的中點時,如圖2,確定線段![]() 與
與![]() 的大小關系,請你直接寫出結論:
的大小關系,請你直接寫出結論:![]() ______
______![]() .(填>,<或=)
.(填>,<或=)
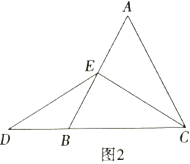
②特例啟發,解答題目,
解:題目中,![]() 與
與![]() 的大小關系是:
的大小關系是:![]() ______
______![]() .(填>,<或=)
.(填>,<或=)
理由如下:如圖3,過點![]() 作
作![]() ,交
,交![]() 于點
于點![]() ,(請你補充完成解答過程)
,(請你補充完成解答過程)
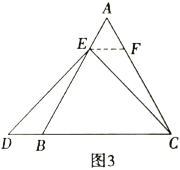
(2)拓展結論,設計新題,
同學小敏解答后,提出了新的問題:在等邊![]() 中,點
中,點![]() 在直線
在直線![]() 上,點
上,點![]() 在直線
在直線![]() 上,且
上,且![]() ,已知
,已知![]() 的邊長為
的邊長為![]() ,求
,求![]() 的長?(請直接寫出結果)
的長?(請直接寫出結果)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com