
如圖10,在平面直角坐標系![]() 中,一動直線
中,一動直線![]() 從
從![]() 軸出發,以每秒1個單位長度的速度沿
軸出發,以每秒1個單位長度的速度沿![]() 軸向右平移,直線
軸向右平移,直線![]() 與直線
與直線![]() 相交于點
相交于點![]() ,以
,以![]() 為半徑的⊙
為半徑的⊙![]() 與
與![]() 軸正半軸交于點
軸正半軸交于點![]() ,與
,與![]() 軸正半軸交于點
軸正半軸交于點![]() .設直線
.設直線![]() 的運動時間為
的運動時間為![]() 秒.
秒.
(1)填空:當![]() 時,⊙
時,⊙![]() 的半徑為 ,
的半徑為 ,![]() ,
,![]() ;
;
(2)若點![]() 是坐標平面內一點,且以點
是坐標平面內一點,且以點![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的四邊形為平行四邊形.
為頂點的四邊形為平行四邊形.
①請你直接寫出所有符合條件的點![]() 的坐標;(用含
的坐標;(用含![]() 的代數式表示)
的代數式表示)
②當點![]() 在直線
在直線![]() 上方時,過
上方時,過![]() 、
、![]() 、
、![]() 三點的⊙
三點的⊙![]() 與
與![]() 軸的另一個交點為
軸的另一個交點為

|

 解:(1)
解:(1)![]() ,
,![]() ,
,![]() ; ………………3分
; ………………3分
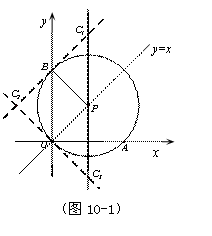
(2)符合條件的點![]() 有3個,如圖10-1,分別為
有3個,如圖10-1,分別為![]() 、
、
![]() 、
、![]() ;…………………………………7分
;…………………………………7分
(3) ![]() 是等腰直角三角形.理由如下:
是等腰直角三角形.理由如下:
當點![]() 在第一象限時,如圖10-2,連接
在第一象限時,如圖10-2,連接![]() 、
、![]() 、
、![]() 、
、![]() .
.
由(2)可知,點![]() 的坐標為
的坐標為![]() ,由點
,由點![]() 坐標為
坐標為![]() ,點
,點![]() 坐
坐
標為![]() ,點
,點![]() 坐標為
坐標為![]() ,可知
,可知![]() ,
,![]()
 是等腰直角三
是等腰直角三![]() 角形,又
角形,又![]() ,進而可得
,進而可得![]() 也是等腰
也是等腰
直角三角形,則![]() .
.
![]() ,
,
![]()
![]() 為⊙
為⊙![]() 的直徑,
的直徑,
![]()
![]() 、
、![]() 、
、![]() 三點共線,
三點共線,
又![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() 為⊙
為⊙![]() 的直徑,
的直徑,
![]()
![]()

![]()
![]()
過點![]() 作
作![]() 軸于點
軸于點![]() ,則有
,則有![]() ,
,
![]()
![]()
![]()
![]() ∽
∽![]()
![]() 即
即![]()
解得![]() 或
或![]()
依題意,點![]() 與點
與點![]() 不重合,
不重合,
![]() 舍去
舍去![]() ,只取
,只取![]()
![]() 即相似比為1,此時兩個三角形全等,
即相似比為1,此時兩個三角形全等,
則![]()
![]()
![]() 是等腰直角三角形.
是等腰直角三角形.
當點![]() 在第二象限時,如圖10-3,同上可證
在第二象限時,如圖10-3,同上可證![]() 也是等腰直角三角形.
也是等腰直角三角形.
綜![]() 上所述, 當點
上所述, 當點![]() 在直線
在直線![]() 上方時,
上方時, ![]() 必等腰直角三角形.
必等腰直角三角形.


科目:初中數學 來源:2013屆江蘇無錫新領航教育咨詢有限公司九年級暑假上課驗收數學試卷(帶解析) 題型:解答題
如圖10,在平面直角坐標系中,正方形OABC邊長是4,點A、C分別在y軸、x軸的正半軸上.動點P從點A開始,以每秒2個單位長度的速度在線段AB上來回運動.動點Q從點B開始沿B→C→O的方向,以每秒1個單位長度的速度向點O運動.P、Q兩點同時出發,當點Q到達點O時,P、Q兩點同時停止運動.設運動時間為t,△OPQ的面積為S.
(1)當t =1時,S = ;
(2)當0≤ t ≤ 2時,求滿足△BPQ的面積有最大值的P、Q兩點坐標;
(3)在P、Q兩點運動的過程中,是否存在某一時刻,使得S = 6.若存在,請直接寫出所有符合條件的P點坐標;若不存在,請說明理由.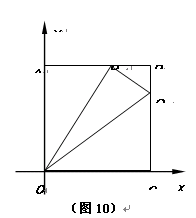
查看答案和解析>>
科目:初中數學 來源:2011年北京市通州區中考二模數學試卷 題型:解答題
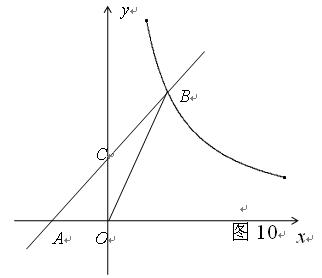
已知:如圖10,在平面直角坐標系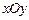 中,直線
中,直線 與
與 軸交于點
軸交于點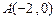 ,與反比例函數在第一象限內的圖象交于點
,與反比例函數在第一象限內的圖象交于點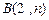 ,連結
,連結 ,若
,若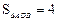 .求該反比例函數的解析式和直線
.求該反比例函數的解析式和直線 的解析
的解析 式.
式.
查看答案和解析>>
科目:初中數學 來源:2012-2013學年江蘇無錫新領航教育咨詢有限公司九年級暑假上課驗收數學試卷(解析版) 題型:解答題
如圖10,在平面直角坐標系中,正方形OABC邊長是4,點A、C分別在y軸、x軸的正半軸上.動點P從點A開始,以每秒2個單位長度的速度在線段AB上來回運動.動點Q從點B開始沿B→C→O的方向,以每秒1個單位長度的速度向點O運動.P、Q兩點同時出發,當點Q到達點O時,P、Q兩點同時停止運動.設運動時間為t,△OPQ的面積為S.
(1)當t =1時,S = ;
(2)當0≤ t ≤ 2時,求滿足△BPQ的面積有最大值的P、Q兩點坐標;
(3)在P、Q兩點運動的過程中,是否存在某一時刻,使得S = 6.若存在,請直接寫出所有符合條件的P點坐標;若不存在,請說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com