Question

【題目】如圖，直線與軸、軸分別相交于點C、B，與直線相交于點A．

（1）求A點坐標；

（2）如果在y軸上存在一點P，使△OAP是以OA為底邊的等腰三角形，求P點坐標；

（3）在直線上是否存在點Q，使△OAQ的面積等于6？若存在，請求出Q點的坐標，若不存在，請說明理由．

Answer 1

【答案】（1）A點坐標是（2，3）；（2）P點坐標是（0，）；（3）存在；點Q是坐標是（（，））或（，））．

【解析】（1）聯立方程，解方程即可求得；

（2）設P點坐標是（0，y），根據勾股定理列出方程，解方程即可求得；

（3）分兩種情況：①當Q點在線段AB上：作QD⊥y軸于點D，則QD=x，根據S△OBQ=S△OAB﹣S△OAQ列出關于x的方程解方程求得即可；②當Q點在AC的延長線上時，作QD⊥x軸于點D，則QD=﹣y，根據S△OCQ=S△OAQ﹣S△OAC列出關于y的方程解方程求得即可．

（1）解方程組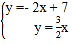：得：，

∴A點坐標是（2，3）；

（2）設P點坐標是（0，y）．

∵△OAP是以OA為底邊的等腰三角形，∴OP=PA，∴22+（3﹣y）2=y2，解得：y=，∴P點坐標是（0，）．

故答案為：（0，）；

（3）存在；

由直線y=﹣2x+7可知B（0，7），C（，0）．

∵S△AOC=××3=＜6，S△AOB=×7×2=7＞6，∴Q點有兩個位置：Q在線段AB上和AC的延長線上，設點Q的坐標是（x，y）．

當Q點在線段AB上：作QD⊥y軸于點D，如圖①，則QD=x，∴S△OBQ=S△OAB﹣S△OAQ=7﹣span>6=1，∴OBQD=1，即×7x=1，∴x=，把x=代入y=﹣2x+7，得y=，∴Q的坐標是（）；

當Q點在AC的延長線上時，作QD⊥x軸于點D，如圖②則QD=﹣y，∴S△OCQ=S△OAQ﹣S△OAC=6﹣=OCQD=，即××（﹣y）=，∴y=﹣，把y=﹣代入y=﹣2x+7，解得x=，∴Q的坐標是（，﹣）．

綜上所述：點Q是坐標是（）或（，﹣）．